vivat2.okis.ru

Локация Главная страница Карта сайта 

С.1.11. Округление натуральных чисел

1. Округлите число 2448 до сотни.

а) 2500;      б) 2450;      в) 2400;       г) 2000

Ответ: в) 2400.

2. Округлите число 82 954:

1) до десятков;            2) до сотен;

3) до тысяч;                 4) до десятков тысяч.

Ответ: 1) 82 950;  2) 83 000;   3) 83 000;  4) 80 000.

3. Округлите число до наивысшего разряда:

1) 46;           2) 907;             3) 4289.

Ответ: 1) 50;  2) 900;  3) 4000.

4. Округлите до метров и до километров:

1) 278 524 см;     2) 4 886 354 см;     3) 78 277 см.

Ответ:  1) 2785 м, 3 км; 2) 48864 м, 49 км; 3) 783 м, 1 км.

5.* При взвешивании овощей, вывозимых с базы, результат округляют до десятков. Запишите показатели массы взвешивания овощей, если было вывезено:

             1) 942 кг;       2) 759 кг;         3) 2148 кг.

Ответ:  1) 940 кг;       2) 760 кг;        3) 2150 кг.

Контрольная работа № 1 к главе 1 «Натуральные числа»

Вариант 1

1.В каком случае верно выполнено сравнение чисел?

а) 70 044 > 700 000          б) 3333  > 3349

в) 6969  <  9696                г) 5297 < 5279

Ответ: в) 6969  <  9696                .

2. Запишите число:

1) девяносто пять тысяч двести восемь4

2) тринадцать миллионов четыреста сорок шесть тысяч двести тридцать девять;

3) пятьсот тысяч;

4) семь миллионов девятьсот шестьдесят один.

Ответ: 1) 95 208; 2) 13 446 239; 3) 500 000; 4) 7 000 961.

3. Представьте в виде суммы разрядных слагаемых число:

1) 378;          2) 6093.

Ответ:1) 378 = 300 + 70 + 8; 2) 6093 = 6000 + 90 + 3.

4. Запишите названия всех отрезков, изображенных на рисунке 81.

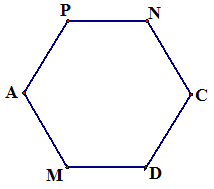
   Рис. 81

Ответ: АР, РN, NC, CD, DM, MA.

5. Запишите все лучи, изображенные на рисунке 82.

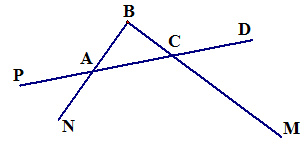
                                                   Рис. 82

Ответ: AP, AN, AD, BN, BM, CD, CP, CM.

6. Начертите отрезок MN и отметьте на нем точку Т. Измерьте получившиеся отрезки.

Решение.

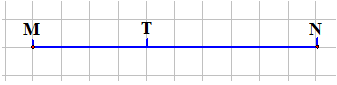
МТ = 2 см, ТN =  3 см.

7. На координатном луче, единичный отрезок которого равен длине одной клеточки тетради, отметьте точки А(3), В(5), К(8), Е(13). На этом же рисунке отметьте точку Т, если ее координата – натуральное число, которое больше 14 и меньше 16.

Решение.

8. Округлите число:

1) 84 749 до тысяч;

2) 89 146 до сотен;

3) 658 366 до десятков тысяч.

Ответ: 1) 85 000; 2) 89 100; 3) 660 000.

9. Округлите:

1) 5375 г до килограммов;       2) 3984 м до километров;

3) 861 кг до центнеров;            4) 7208 кг до тонн; 

5) 3 м 411 мм до метров;          6) 36 902 м² до гектаров.

Ответ:1) 5 кг; 2) 4 км; 3) 9 ц; 4) 7 т; 5) 3 м; 6) 4 га.

10. Запишите пятизначное число, которое оканчивается цифрой 3 и меньше числа 10 013.

Ответ: 10 003.

11.* Запишите при помощи цифр 2, 5, 9 все трехзначные числа (цифры в записи числа не должны повторяться) и расположите их в порядке убывания.

Ответ: 952, 925, 592, 529, 295, 259.

12.* Имеется 6 детских шаров: синих меньше, чем зеленых, желтых больше, чем зеленых. Шаров какого цвета больше, чем других цветов? Сколько имеется шаров каждого цвета?

Решение. Синих шаров < зеленых шаров < желтых шаров. Значит, желтых шаров больше, чем других цветов. Так как 1< 2 < 3  и 1 + 2 + 3 = 6, то синих шаров – 1, зеленых шаров – 2, желтых шаров – 3. 

Ответ:больше желтых шаров; синих шаров – 1, зеленых шаров – 2, желтых шаров – 3.

С.1.3. Точка, прямая, плоскость

1.Назовите точки, не лежащие на прямой (рис. 1).

Рис. 1

а) точки А и В              б) точки С и D

в) точки А и D              г) точки В и С

Ответ: в) точки А и D.

2. Начертите в тетради любые две прямые и обозначьте их малыми буквами латинского алфавита.

Решение.

Прямые   а   и   b.

3. Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько прямых получилось?

Решение.

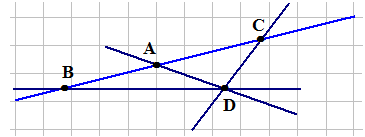
Получились прямые  ВС, ВD,AD,CD. Их 4.

Ответ: 4.

4. На сколько частей делят плоскость две прямые а и b, изображенные на рисунке 2?

Рис. 2

Решение.

Прямые а и b бесконечны, т. е. имеем:

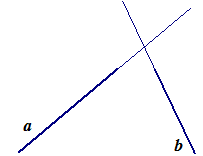
Значит, прямые а и b делят плоскость на 4 части.

Ответ: на 4.

5.* На прямой отмечены точки А, В, С так, что расстояние между точками А и В равно 27 мм, между А и С – 11 мм, между В и С – 16 мм. Какая из этих точек лежит между двумя другими?

Решение.

АВ = 27 мм, АС = 11мм, ВС = 16мм.

27 = 11 + 16, т. е.  АВ = АС + СВ.

Значит, точка С лежит между точками А и В.

Ответ: точка С лежит между точками А и В.

 С.1.4. Запись натуральных чисел

1.Среди чисел 2483, 4238, 3842, 8324 найдите число, в котором цифра 8 находится на позиции сотен.

а) 2483    б) 4238    в) 3842     г) 8324

Ответ: в) 3842.   

2. Из каких цифр состоит запись числа и сколько среди них различных:

1) 45 350;   2) 2 121 212;   3) 7892?

Ответ:

1) Запись числа 45 350 состоит  из пяти цифр, среди них 4 различных;

2) Запись  числа 2 121 212  состоит  из семи цифр, среди них 2 различные;

3) Запись числа 7892 состоит  из четырех цифр, среди них 4 различных.

3. Найдите разность наименьшего трехзначного числа и  наибольшего двузначного числа.

Решение.

 100 – 99  = 1.

Ответ: 1.

4. Укажите все двузначные числа, в записи которых сумма цифр равна 3.

Ответ: 12, 21, 30.

5.* Из какого  четырехзначного числа надо вычесть 10, чтобы получилось наибольшее трехзначное число?

Решение.

Наибольшее трехзначное число 999. Следовательно, 999 + 10 = 1009 – искомое четырехзначное число. Действительно,  1009 – 10 = 999.

Ответ: 1009.

С.1.5. Разряды в записи числа

1.   Запишите число, в котором 6 единиц шестого разряда, 3 единицы четвертого разряда, 1 единица третьего разряда, 8 единиц второго разряда.

а) 603 180    б) 631 800    в) 630 018     г) 600 318

Ответ:а) 603 180.

2. Запишите три раза подряд число 84. Сколько единиц пятого разряда содержится в этом числе?

Решение.

848484. Единиц пятого разряда 4

Ответ: 4.   

3. Сколько единиц третьего разряда содержится в числе, полученном при сложении чисел 9999 и 1111?

Решение. 9999 + 1111 = 11110. В третьем разряде числа 11110 содержится 1 единица.

Ответ: 1.

4. Представьте в виде суммы разрядных слагаемых число:

а) 299;     б) 4455;     в) 80 808.

Ответ: а) 299  = 200 + 90 + 9;    

            б) 4455 = 4000 + 400 + 50 + 5;

            в) 80 808  = 80 000 + 800 + 8 .

 5.* Сколько всего существует трехзначных чисел, запись которых начинается цифрой 1?

Решение. 100, 101, 102, …, 199. Всего таких чисел 100.

Ответ: 100.

С.1.6. Классы в записи и чтении числа

1.Запишите цифрами число: тридцать две тысячи пятьдесят восемь.

а) 32 058                 в) 3285

в) 302 805               г) 32 805

Ответ:   а) 32 058.

2. Какая цифра в записи числа 123 456 789 записана на месте:

1) разряда сотен класса единиц;

2) разряда единиц класса тысяч;

3) разряда  десятков класса миллионов?

Ответ: 1) 7; 2) 6; 3) 2.

3. Запишите цифрами число, состоящее:

1) из 7 десятков тысяч и 64 сотен;

2) из 20 десятков тысяч и 5023 сотен;

3) из 10 десятков миллионов 3600 тысяч и 1111 сотен.

Решение.

1)70 000 + 6400 = 76 400;

2) 200 000 + 502300 = 702 300;

3) 100 000 000 +3600 000 + 111100  = 103 711 100.

Ответ: 1) 76 400; 2) 702 300;  3) 103 711 100.

4. Сколько тысяч содержится:

1) в 8 сотнях тысяч;

2) в 4 десятках тысяч и 5 тысячах;

3) в 3 сотнях тысяч 9 десятках тысяч и 7 сотнях?

Ответ:

1) в 800 000 содержится 800 тысяч;

2) в 45 000 содержится 45 тысяч;

3) в 390 700 содержится 390 тысяч.

5.* Число представлено в виде суммы разрядных слагаемых: 500 + 20 + 1. Запишите в виде суммы разрядных слагаемых число, которое получается  из данного числа, если к нему приписать справа:

1) один нуль:

2)два нуля;

3) три нуля.

Ответ:

1) 5210 = 5000 + 200 +10;

2) 52100 = 50 000 + 2 000 + 100;

3) 521000 = 500 000 + 20 000 + 1 000.

Дистанционная олимпиада по математике!

1.Для нумерации страниц в учебнике потребовалось 787 цифр. Какой номер имеет последняя пронумерованная страница, если первая пронумерованная страница имеет номер 3?

Решение.

Однозначных чисел (3, 4, 5, 6, 7, 8, 9) всего 7.

Двузначных чисел (10, 11, 12, …, 99) всего 90.

На нумерацию страниц однозначными и двузначными числами использовано 7 + 90·2 = 187 цифр.

Значит, на нумерацию трехзначными числами пошло 787 – 187 = 600 цифр, а чисел –  600: 3 =  200. Отсчитаем 200 трехзначных чисел: первое такое число 100, прибавим к нему  еще 199 и получим последнее трехзначное число 299. Следовательно, последняя пронумерованная страница имеет номер 299.  

Ответ:номер 299.

2.На лугу ребята пасут жеребят. Если пересчитать ноги ребят и жеребят, то получится 184, а если считать головы, то 53. Сколько на лугу ребят и сколько жеребят?

Решение.

Пусть все жеребята встанут на задние ноги, тогда все (ребята и жеребята) будут стоять на двух ногах и их будет 53·2 = 106. Тогда 184 – 106 = 78 – количество поднятых ног жеребятами и 78:2 = 39 – количество жеребят на лугу. Следовательно, 53 – 39 = 14(ребят).

Ответ:14 ребят, 39 жеребят.

3.Гусеница ползла вверх по дереву. За день она успевала проползти 3 м, а за ночь опускалась на 2 м. На какой день она достигла высоты 7 м?

Решение.

За сутки (за день и ночь) гусеница поднималась на  3 – 2 = 1(м).

За 4 суток она поднимется на 1·4 = 4 (м).

 На 5-й день она поднимется на 4 + 3 = 7 (м).

Ответ: на 5-й день.

4. Из 10 листиков бумаги некоторые разрезали на 4 части. Получили всего 31 листик. Сколько листиков бумаги разрезали?

Решение.

Если разрезать 1 листик на 4 части (останется 9 целых листиков),   то получим  4 + 9 = 13 листиков.

Если любые из 2 имеющихся листиков разрезать на 4 части, то получится   4·2 + 8 = 16 листиков.

Если любые из 3 имеющихся листиков  разрезать  на  4 части,  то    получится  

4·3 + 7 = 19 листиков.

31 листик получится, если  любые из 7 имеющихся листиков разрезать на 4 части каждый (4·7 + 3 = 31).

Ответ:7 листиков.

5.Собака преследует зайца, который находится впереди нее на 40 своих прыжков. Собака делает 7 прыжков за то время, за которое заяц делает 9 прыжков, но 3 прыжка собаки равны 5 прыжкам зайца. Сколько прыжков надо сделать собаке, чтобы догнать зайца?

Решение.По условию 3 прыжка собаки равны 5 прыжкам зайца, следовательно, 21 прыжок собаки равен 35 прыжкам зайца. Заметим, что собака делает 7 прыжков за то время, за которое заяц делает 9 прыжков, значит,  собака делает 21 прыжок за то время, за которое заяц делает 27 прыжков. Известно, что 21 прыжок собаки равен 35 прыжкам зайца, следовательно, собака, сделав 21 прыжок, приближается к зайцу на 8 заячьих прыжков. Сделав 105 прыжков, собака приблизится к зайцу на 40 заячьих прыжков, т. е. догонит зайца.

Другая запись  решения

1 прыжок собаки обозначим 1с, 1 прыжок зайца – 1з.

7с – 9з, а 3с = 5з.

НОК(3;7) = 21

21с – 27з, а 21с = 35з

35з – 27з = 8з – на столько  приблизилась собака.

8з·5 = 40з, когда 21с·5 = 105с.

Ответ: 105 прыжков  собаки.

Текст
для проведения вступительных испытаний
в 5 класс гимназии по математике


1 вариант

1.Найдите значение выражения.

864 : 36 · 406 – 7 048

2. Выполните задание.
Подберите два значения переменной, при которых неравенство а · 60 < 480 будет истинным.
3. Выполните действия с величинами.

14 км 100 м + 2 км 900 м

27 т 300 кг – 5 т

16 ч 12 мин + 65 мин
4. Решите задачу.
На уроке математики Маша выполнила письменное задание за 17 мин, а устное задание на 6 мин 12 с быстрее. Сколько времени затратила Маша на выполнение двух заданий?
5. Решите задачу.
Какой длины потребуется проволока для прямоугольной рамки, если длина рамки 250 мм, а ширина равна 1/5 длины?

Ответы: 1. 2 696; 2. Например, 0 и 1; 3. 17 т; 22 т 300 кг; 17 ч 17 мин; 4. 27 мин 48 с; 5. 600 мм.

Тема урока: Натуральные числа и нуль. Натуральный ряд

Девиз урока: Математика - царица всех наук

Виктор Гюго: "Он скользил, карабкался, падал, поднимался, нащупывал дорогу и упорно шел вперед — вот и все. В этом тайна всякой победы". 

Важно знать: Числа, возникающие при счете, называются натуральными. Число 0 (нуль) не  является натуральным числом. Натуральный ряд - это ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ... В этом ряду первым числом является 1, для каждого числа существует следующее за ним число, нет последнего числа, он бесконечен. Каждое число, кроме 1, имеет предшествующее ему число, на 1 меньшее.

Тема урока:Точка, прямая, плоскость 

Девиз урока: В математику тропинки одолеем без запинки 

Амели Нотомб: "Не опускай руки, ибо рискуешь сделать это за минуту до того, как произойдёт чудо". 

Важно знать: Через любые две точки можно провести прямую, и только одну.
Самостоятельные работы 

Вариант 1

Глава 1. Натуральные числа

С.1.1. Натуральные числа            

1. Укажите выражение, значение которого не является натуральным числом.

а) 24 + 9 – 11                     б) 100:5:20          

в) (21 – 13)*8                     г) 3*4 – 6*2

Ответ: г) 3*4 – 6*2 = 0.

2. Запишите первые пять натуральных двузначных чисел.

Ответ: 10, 11, 12, 13, 14. 

3. Начертите отрезок, длина в сантиметрах которого равна значению выражения:

1) 5*5 – 7*3;                        2) 3 + (18 - 6 ):3.

Решение. 1) 5*5 – 7*3 = 25 – 21 = 4 (см);                      

                2) 3 + (18 - 6):3 = 3 + 12:3 = 3 + 4 = 7(см).    

4. В магазин «Матрешка» привезли 100 коробок с куклами, трансформерами и мягкими игрушками. Из них 30 коробок – с куклами, коробок с трансформерами – в в 2 раза меньше, чем коробок с куклами, а остальные коробки – с мягкими игрушками. Сколько коробок с мягкими игрушками привезли в «Матрешку»?

Решение. 1) 30:2 = 15(коробок) – с трансформерами.

                2) 30 + 15 = 45(коробок) – с трансформерами и куклами.

                3) 100 – 45 = 55 (коробок) – с мягкими игрушками.

Ответ: 55 коробок.

5.* Расставьте скобки таким образом, чтобы равенство 13 – 4:3 + 2*5 – 1 = 11 было верным.

Решение. 4 не делится на 3, а  (13 – 4):3 =3. До 11не хватает еще 8, но 2*(5 – 1) = 8. Поэтому получаем верное равенство (13 – 4):3 + 2*(5 – 1) = 11.

Ответ:  (13 – 4):3 + 2*(5 – 1) = 11.

С.1.2. Натуральный ряд             

Вариант 1 

1.Укажите натуральный ряд.

а) 1, 2, 3, 4, 6, 5, 7, 9, 8, …

б) 1, 2, 3, 4, 5, 6, 7, 8, 9, …

в) 2, 3, 4, 5, 6, 7, 8, 9, 10, …

г) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …

Ответ: б) 1, 2, 3, 4, 5, 6, 7, 8, 9, …

2. Запишите число, которое следует за числом:

1) 299;                           2) 558;

3) 773;                           4) 1009.

Ответ: 1) 300; 2) 559; 3) 774; 4) 1010.

3. Запишите все натуральные числа, которые больше 348 и меньше 353.

Ответ: 349, 350, 351, 352.

4. Укажите выражение, значение которого является наименьшим натуральным числом.

а) 2*10 – 19 + 23             б) 28:7 + 4*13

в) (7*7 – 6)*6 – 57          г) (14*9 – 15*7)*2

Решение.

а) 2*10 – 19 + 23 = 20 – 19 + 23 = 24

б) 28:7 + 4*13 = 4 + 52 = 56

в) (7*7 – 6)*6 – 57 =(49 – 6)*6 – 57 =  43*6 – 57 = 258 – 57 = 201

г) (14*9 – 15*7)*2 = (126 – 105)*2 = 21*2 = 42

Ответ: а) 2*10 – 19 + 23.

5.* Младшая сестра Ивана загадала ему загадку: «Я задумала однозначное натуральное число. Следующее за ним число тоже однозначное. Какое число я задумала?» Ответьте на ее вопрос. Сколько решений имеет задача?

Решение.

Сестра задумала одно из чисел: 1, 2, 3, 4, 5, 6, 7, 8. Задача имеет 8 решений.

Ответ: 1 или 2, 3, 4, 5, 6, 7,8. Задача имеет 8 решений.