vivat2.okis.ru

Локация Главная страница Карта сайта

Весомость заданий Шкала перевода баллов Продолжение шкалы перевода

Число "е" в № 7 ЕГЭ по математике

Прототипы задания 7 профиля ЕГЭ - 2021

Тема заданий № 7  "Про­изводная и первообразная"

Типы заданий № 7: Геометрический смысл производной, касательная. Физический смысл производной. Применение производной к исследованию функций. Первообразная

За  задание № 7 можно получить 1 балл. На решение дается около 5 минут. Уровень сложности: базовый. Средний процент выполнения: в 2019 году 61.5%, в 2020 году 63,0%. Ответом к заданию 7 по математике должно быть целое число или конечная десятичная  дробь. Требования ФИПИ к профильному уровню  здесь

Кодификатор элементов содержания по математике - классификатор базовой части 

3.2.5. Точки экстремума функции здесь 4.2.1. Применение производной к исследованию функций и построению графиков здесь 4.3.1 Первообразные элементарных функций здесь здесь

В задании № 7 требуется решить одну из задач вышеперечисленного типа. Особенности задания. При подготовке к экзамену следует повторить таблицу производных и правила дифференцирования и обратить внимание на различия в понятиях точка экстремума, экстремум, координаты точки экстремума, наибольшее и наименьшее значение функции. Задания типа № 7 представляет собой задачи на определение поведения функции или ее производной по графику этой функции или ее производной; задачи на определение понятия первообразной и умению выразить площадь криволинейной трапеции через значения первообразной.  Полезные советы. Важно внимательно следить за тем, график какой функции дан и про какую функцию поставлен вопрос задачи. Анализируя график производной, не путайте его с графиком самой функции. Следует тщательно проверять все выкладки, так как при проведении расчетов возможны вычислительные ошибки. Для решения задания № 7 надо знать следующие вопросы: 1. Производная числа, линейной и степенной функции здесь 2. Правила дифференцирования здесь 3. Производная многочлена здесь  4. Уравнение прямой здесь 5. Уравнение касательной к графику функции здесь 6. Физический смысл производной здесь 7. Монотонность и экстремумы функции. 8. Первообразная здесь  9. Криволинейная трапеция и ее площадь здесь

Производная – скорость изменения функции. Производная положительна на промежутках, на которых функция возрастает и отрицательна на промежутках, на которых функция убывает.

Пусть дан график производной функции, определенной во всех точках некоторого промежутка. Существование конечной производной означает дифференцируемость функции на этом промежутке, а значит, влечет существование и непрерывность самой функции на нем. Тогда для определения поведения функции по знаку ее производной можно использовать следующие утверждения: если производная функции положительна на некотором промежутке, то функция возрастает на нем; если производная функции отрицательна на некотором промежутке, то функция убывает на нем; если производная функции в некоторой точке меняет знак с плюса на минус, то функция имеет в этой точке максимум; если производная функции в некоторой точке меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

Максимумы, минимумы и экстремумы функций здесь здесь

Как найти  экстремумы функции по графику производной здесь здесь

Как найти  максимумы или минимумы функции по графику производной  здесь здесь

Как связаны значение производной и поведение функции  здесь

График функции и поведение производной

График производной и поведение функции

Все, что нужно знать о применении производной к исследованию функций здесь

Геометрический смысл производной здесь 

Как найти угловой коэффициент касательной к графику функции в точке Х₀ или (что то же самое) тангенс угла наклона касательной в точке Х₀ здесь  здесь  

Обратите внимание на то, что здесь прямоугольный треугольник с желтыми катетами – лишь вспомогательный инструмент. Суть задачи – найти отношение вертикального изменения функции к приращению аргумента. Для этого надо разбить решение задачи на нахождение углового коэффициента касательной (значения производной функции в точке) на два этапа: первый этап – определение знака; второй этап – определение модуля значения производной.

Тригонометрические функции острого угла прямоугольного треугольника – это не только часть планиметрических задач №3 и №6, но и ряд задач про геометрический смысл производной (№7), задачи, где требуется вычислить значения тригонометрических функций (№ 9 и даже № 10).

За задачу 7 получите 0 баллов, если перепутаете график функции с графиком производной. 

Задачи  с ответами для самостоятельного решения и  самопроверки,

предлагаемые авторами ЕГЭ на экзаменах прошлых лет, а также из открытого банка ФИПИ:

1. 2021 год. Демонстрационный вариант ЕГЭ. На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, ..., x₉. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

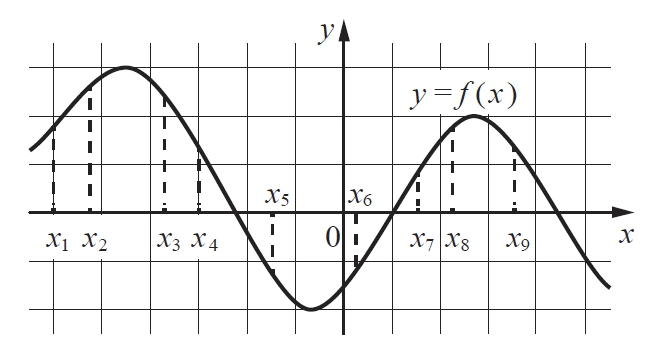 Решение здесь

ИЛИ

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀ . Найдите значение производной функции f(x) в точке x₀ . Решение здесь

1. 2020 год, основная волна ЕГЭ, Москва. На рисунке изображен график функции  и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

Решение здесь или здесь

2. 2020 год, досрочная волна ЕГЭ. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

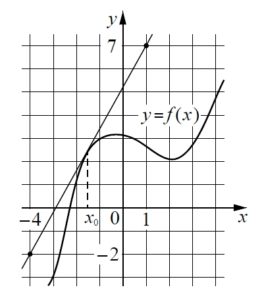Решение здесь

3. 2019 год. Основная волна ЕГЭ. Центр. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Решение здесь + здесь

4. 2018 год. Основная волна ЕГЭ.  На рисунке изображен график производной функции f(x), определенной на отрезке [−10;37]. Найдите количество точек максимума функции f(x) на отрезке [0;37].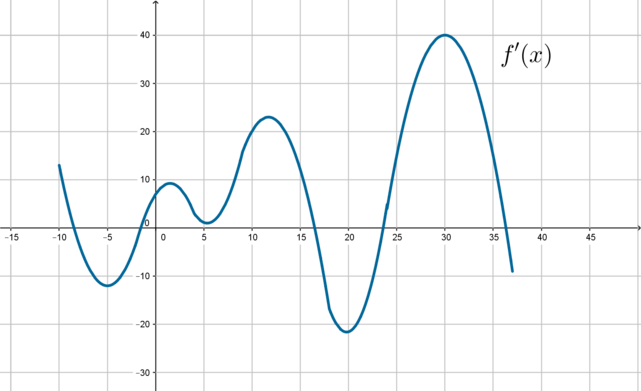
 Решение здесь

5. 2017 год. Основная волна ЕГЭ.  На рисунке изображен график производной функции y=f(x). На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. В скольких из этих точек функция f(x) возрастает?

Решение здесь

Геометрический смысл производной: уравнение касательной

Прямая y=7x−5 параллельна касательной к графику функции y=х²+6x-8. Найдите абсциссу точки касания.  Решение здесь  Прямая y=−4x−11 является касательной к графику функции y=x^3+7x^2+7x-6. Найдите абсциссу точки касания. Решение здесь  Прямая y=3x+1 является касательной к графику функции f(x) = ax^2+2x+3. Найдите a. Решение здесь  Прямая y=−5x+8 является касательной к графику функции f(x) = 28x^2+bx+15. Найдите b учитывая, что абсцисса точки касания больше 0. Решение здесь Прямая y=3x+4 является касательной к графику функции f(x) = 3x^2-3x+c. Найдите c. Решение здесь На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

  Решение здесь

На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

  Решение здесь

На рисунке изображён график функции f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀. 

  Решение здесь

На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

  Решение здесь

На рисунке изображен график функции y=f(x), определенной на интервале (−6;8). Определите количество целых точек, в которых производная функции положительна.

Решение здесь

На рисунке изображен график функции y=f(x) , определенной на интервале (−5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна.

 Решение здесь

На рисунке изображен график функции y=f(x), определенной на интервале (−8;3). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней.

 Решение здесь

На рисунке изображен график функции y=f(x), определенной на интервале (−2;12). Найдите сумму точек экстремума функции f(x).

 Решение здесь

На рисунке изображен график функции y=f(x), определенной на интервале (−3;9). Найдите количество точек, в которых производная функции f(x) равна 0.

 Решение здесь

Физический смысл производной здесь

Тесты: 1) здесь 2)здесь ответ здесь 3)здесь ответ здесь  4) здесь здесь 5) здесь ответ здесь 6) здесь ответ здесь 7) здесь ответ здесь

Первообразная и определенный интеграл

Таблица первообразных здесь Геометрический смысл определенного интеграла здесь

На рисунке изображён график функции y=F(x) – одной из первообразных функции f(x), определённой на интервале (−3;5). Найдите количество решений уравнения f(x)=0 на отрезке [−2;4].

Решение здесь

На рисунке изображён график функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)−F(2), где F(x) – одна из первообразных функции f(x).

Решение здесь

На рисунке изображён график некоторой функции y=f(x). Функция F\(x)=x^3+30x^2+302x-15/8 – одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.

 Решение здесь

На рисунке изображён график некоторой функции y=f(x). Функция F(x)=-x^3-27x^2-240x-8 – одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Решение здесь

Еще 5 задач с первообразной:

1. Условие Решение и ответ

2. Условие Решение и ответ

3. Условие Решение и ответ

4. Условие Решение и ответ

5. Условие Решение и ответ

Чтобы продолжить подготовку к ЕГЭ 2021, перейдите по ссылкам на другие страницы сайта:

Локация Главная страница Карта сайта

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail:  [email protected]