vivat2.okis.ru

Локация Главная страница Карта сайта

Готовься к олимпиаде по математике

Этот базовый курс олимпиадной математики для  учащихся 4 класса включает в себя темы: логика, множества, комбинаторика, игры и стратегии, рыцари и лжецы, конструкции, геометрия, разные задачи.

Олимпиадная математика — штука особенная, можно сказать, отдельная дисциплина. Ведь здесь на первое место выходят не аккуратность и умение считать, а нестандартные методы и подходы. Предлагаемые ниже материалы предназначены для учителей, а также для  учащихся,  которые желают стать настоящими чемпионами и не боятся нестандартных задач.

Логика

1. Из каюты капитана пиратского корабля исчезла бутылка ямайского рома. Подозрение пало на Гарри, Тома и Одноглазого Чарли. Подозреваемые заявили: Гарри: не трогал я Вашего рома. Том тоже ни при чём. Том: ручаюсь головой, сэр, Гарри невиновен. Ром стянул Одноглазый. Чарли: бутылочку Вашу взял Гарри. А я в этом не замешан. Капитану удалось выяснить, кто взял ром. Оказалось, что один из подозреваемых дважды солгал, другой — дважды сказал правду, а третий один раз солгал, а другой раз сказал правду. Кроме того, вор действовал в одиночку. Кто же он? Решение Ответ

2. Аня, Вера и Серёжа занимались в разных кружках: танцевальном, хоровом и драматическом. На вопрос, кто в каком кружке занимается, они ответили: Аня: Я — в танцевальном. Вера: Я — не в танцевальном. Серёжа: Я — не в хоровом. Засмеявшись, добавили: Вы ведь из математического кружка, вот и определите, в каком кружке каждый из нас занимается, учитывая, что из трёх ответов один верный, а два — нет. Ответ

3. Дружили три товарища: Белов, Рыжов и Чернов. Волосы у одного из них были белые, у другого - рыжие, у третьего - черные. - Интересно, - заметил черноволосый, - что цвета наших с тобой волос не соответствуют нашим фамилиям. - А ведь верно, но мне подошла бы твоя фамилия, - подтвердил Белов. Какой цвет волос у каждого? Ответ

4. До царя дошла весть, что кто-то из трёх богатырей убил Змея Горыныча. Приказал царь им всем явиться ко двору. Молвили богатыри: Илья Муромец: — Змея убил Добрыня Никитич. Добрыня Никитич: — Змея убил Алёша Попович. Алёша Попович: — Я убил змея. Известно, что только один богатырь сказал правду, а двое слукавили. Кто убил змея? Ответ

5. Из сейфа похищены важные документы. Полиция уверена, что в краже участвовали двое из семерых подозреваемых: А, Б, В, Г, Д, Е, Ж. По показаниям консьержки дома напротив один из похитителей был высокого роста. Шерлок Холмс, осмотрев место происшествия, обнаружил пепел сигары и несколько волосков собаки. По характерным царапинам на сейфе он определил, что взломщик — левша. А, Б, В и Г высокие; все, кроме А курят сигары; Д и Ж держат дома собак, а А и Е — левши. На основании всех улик инспектор Лестрейд арестовал А и Д. Правильно ли он поступил? Ответ

6. Перед футбольным матчем команд «Север» и «Юг» было дано пять прогнозов:
а) ничьей не будет;
б) в ворота «Юга» забьют;
в) «Север» выиграет;
г) «Север» не проиграет;
д) в матче будет забито ровно 3 гола.
После матча выяснилось, что ровно три прогноза оказались верными. С каким счетом закончился матч? Ответ

7. Четыре подруги пришли на каток, каждая со своим братом. Они разбились на пары и начали кататься. В каждой паре кавалер выше дамы, и никто не катается со своей сестрой или братом. Самый высокий из компании —Юра Воробьёв, следующий по росту — Андрей Егоров, потом Люся Егорова, Серёжа Петров, Оля Петрова, Дима Крымов, Инна Крымова и Аня Воробьёва. Кто с кем катался? Ответ

8. Три гнома - Пили, Ели и Спали - нашли в пещере алмаз, топаз и медный таз. У Ели капюшон красный, а борода длиннее, чем у Пили. У того, кто нашел таз, самая длинная борода, а капюшон синий. Гном с самой короткой бородой нашел алмаз. Кто что нашел, если каждый гном нашел один предмет? Ответ

9. Петя, Дима, Гена и Вова занимаются в спортивных секциях : гимнастической, Баскетбольной, волейбольной и легкой атлетики. Волейболист старше Пети и Димы, но учится с ними в одном классе. Петя и Гена на тренировки ходят пешком вместе, а гимнаст ездит на автобусе. Легкоатлет не знаком ни с баскетболистом, ни с волейболистом. Кто в какой секции занимается?  Ответ

10. Ворона, Павлин и Попугай принесли на выставку по одной свей картине: портрет орла, натюрморт с сыром и абстрактную композицию. Известно, что ни Ворна, ни Павлин никогда не пишет портретов, а Попугай натюрмортов. Определите автора каждой картины. Ответ

Связка задач

1. В классе 20 пловцов, 14 борцов и 10 футболистов. Каждый спортсмен занимается ровно двумя из этих видов спорта. Сколько всего в классе спортсменов? Ответ

2. Лёша хочет вычеркнуть из числа 1329870 три цифры так, чтобы получилось наименьшее число. Покажите, как ему это сделать. Ответ

3. Вот несколько числительных, записанных по-венгерски: 43 - negyven három, 58 - ötven nyolc, 375 - háromszáz hetven öt, 197 - száz kilencven hét, 246 - kétszáz negyven hat, 284 - kétszáz nyolcven négy Запишите цифрами: háromszáz negyven nyolc. Ответ

4. Пятачок, Иа-Иа и Винни-Пух считали морковки на двух грядках Кролика: Пятачок: «На первой грядке морковок больше 18. На второй — не больше 14». Иа-Иа: «На первой меньше 20. На второй ровно 14». Винни-Пух: «На первой ровно 17. На второй больше 14». Известно, что один из них оба раза ошибся, а два других оба раза были правы. Сколько морковок на грядках (обеих в сумме)? Ответ

5. Несколько гномов, навьючив свою поклажу на пони, отправились в дальний путь. Их заметили тролли, которые насчитали в караване 36 ног и 15 голов. Сколько было гномов, и сколько пони? Ответ

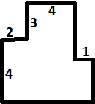
6. На чертеже изображён маршрут лыжной прогулки и некоторые расстояния (в км) между поворотами. Найдите полную длину дистанции лыжников.

     Ответ

7.После того, как туристы прошли 1 км, а затем половину оставшегося пути, им осталось пройти треть всего пути и 1 км. Чему равен весь путь? Ответ

8. Сколько раз за сутки минутная стрелка обгоняет часовую? Ответ

9. Какой цифрой заканчивается разность 1·2·3·4·….·2012·2013·2014 – 1·3·5·….·2011·2013 ? Ответ

10. На доске нарисованы два круга, внутри которых отмечено несколько точек. Внутри первого из них всего 190 отмеченных точек. Внутри второго — всего 230 отмеченные точки. Внутри обоих кругов одновременно находится ровно 70 точек. А сколько отмеченных точек всего? Ответ

11. Александра Ефремовна загадала число от 7 до 70. Ей можно задавать вопросы, на которые можно ответить «да» или «нет». Сколько вопросов понадобится, чтобы гарантированно отгадать число? Ответ

12. Под крышкой каждой бутылки мехмат-колы нарисована одна из трех картинок: звездочка, карандаш или рожица. Если собрать две крышки с одинаковыми картинками, то их можно обменять в буфете на шоколадку. Сколько бутылок надо купить, чтобы точно получить две шоколадки? Ответ

13. Каникулы начались 2 июля, а закончились 29 августа. Сколько дней длились каникулы? Ответ

14. У Насти и Ани денег поровну. Сколько денег должна дать одна из них другой, чтобы у Насти стало на 10 рублей больше, чем у Ани? Ответ

15. Три землекопа за 2 часа вырыли 3 ямы. Сколько ям выроют 6 землекопов за 5 часов? Ответ

Режем колбасу и не только

Множества

1. Среди купленных конвертов было 15 голубых и 10 с марками. На 5-и голубых конвертах были марки. Сколько куплено конвертов? Ответ

2. В саду у Ани и Вити росло сто розовых кустов. Витя полил половину всех кустов, и Аня полила половину всех кустов. При этом оказалось, что ровно три куста, самые красивые, были политы и Аней, и Витей. Сколько розовых кустов остались неполитыми? Ответ

3. На столе яблок на 4 меньше, чем яблок и груш вместе, а груш на 7 меньше, чем яблок и груш вместе. Сколько всего фруктов на столе? Сколько яблок? А груш?  Ответ

4. В пакете лежат фрукты. Все, кроме двух, апельсины. Все, кроме двух, яблоки. Все, кроме двух, бананы. Сколько каких фруктов в пакете? Ответ

5. Седьмая часть всех попугаев умеет говорить; пятая часть всех говорящих животных — попугаи. Кого больше: попугаев или говорящих животных? Ответ

6. Вася посчитал число коробочек, в которых один шарик или больше: их оказалось 8; коробочек, в которых больше одного шарика - 6; больше двух шариков - 5; больше трех - 3; больше четырех - 2. Коробочек, в которых больше пяти шариков, не было. Найдите общее число шариков во всех коробках. Ответ

7. В классе 17 пловцов, 6 борцов и 13 футболистов. Каждый спортсмен занимается ровно двумя из этих видов спорта. Сколько всего в классе спортсменов? Ответ

8. В классе 27 пловцов, 10 борцов и 15 футболистов. Каждый спортсмен занимается ровно двумя из этих видов спорта. Сколько всего в классе спортсменов? Ответ

9. На прогулку пошли четвероклассники и пятиклассники. Все они были либо босиком, либо в тапочках. Четвероклассников было 24, а босых учеников 16. Обутых пятиклассников было столько же, сколько босых четвероклассников. Сколько учеников ходили на прогулку? Ответ

10. В каждый из четырех походов ходила группа из 20 человек. Во все 4 похода ходили 10 человек. Ровно в 3 похода ходили 9 человек. Ровно в 2 похода ходили 5 человек. Сколько человек ходило только в 1 поход? Ответ

Комбинаторика для полярников

1. В тренировочной гонке на собачьих упряжках участвуют северные жители Анука, Нанук и Кавак. Назовите возможные варианты распределения призовых мест. Ответ

2. Из поселка Мурмаши в поселок Туманный Мурманской области ведет 5 дорог, из поселка Туманный в поселок Умба — 6 дорог. Сколько способов добраться из поселка Мурмаши в Умбу? Ответ

3. Тем временем из Москвы отправилась экспедиция на Северный Полюс. Первый этап пути можно преодолеть на поезде или на самолете. Второй этап — на ледоколе, вертолете или дирижабле. И третий этап пути — на собачьих упряжках или на лыжах. Какие возможные варианты путешествия есть у полярников? Ответ

4. В языке арктических снеговиков 4 буквы, слово — любая последовательность из этих букв (длины 4, все буквы должны быть разные). Сколько у них слов? Ответ

5. В экспедицию на Северный Полюс отправилось 11 человек. Нужно выбрать командира и заместителя. Сколькими способами это можно сделать? Ответ

6. Даниил закрыл свой рюкзак с дневником экспедиции на замок с секретным кодом, составленным из двух цифр и обратил внимание, что сумма этих цифр равна 10. Утром он забыл этот код, но, к счастью, запомнил сумму цифр кода. Он решил выписать все возможные варианты на листочке. Сколько пройдет времени, и Даниил наверняка сможет достать свой дневник, если на проверку одного кода ему нужна 1 минута? Ответ

7. В магазине походного снаряжения «Экспедиция» продается 5 спальников, 3 палатки и 4 рюкзака.
а) Сколькими способами можно снарядиться (купить все три предмета)?
б) А если денег хватает только на два предмета, сколько есть способов купить любые два из них?Ответ

8. Тушенка, гречка, сгущенка и хлеб лежат в палатке в ряд. Гречка не в начале и не в конце этого ряда. Стоя лицом к этому ряду, можно увидеть, что гречка — справа от хлеба (но не обязательно рядом с ним). Сколько разных вариантов расположения продуктов может быть? Ответ

9.  6 полярников составляют расписание дежурства на ночь. Сколькими способами их можно расположить в списке? Ответ

Игры и стратегии

Чтобы сдать задачу, нужно обыграть преподавателя в игру из задачи. Тренируйтесь друг с другом и помните, что количество попыток на сдачу задачи ограничено! (Это не касается задач, помеченных звёздочками. Их надо сдавать как обычно.)

1. а) В кучке лежит 10 спичек. Игроки по очереди берут спички из кучки. За один ход разрешается взять 1 или 2 спички. Проигрывает тот, кто не может сделать ход.
б) То же самое, но в кучке 12 спичек.
в) То же самое, но в кучке 20 спичек, и можно брать от 1 до 4 спичек зараз.
г) (*) Сформулируйте общую стратегию игры, когда можно брать от 1 до k спичек. Решение

2. Это  задача наоборот.
а) В кучке лежит 10 спичек. Игроки по очереди берут спички из кучки. За один ход разрешается взять 1 или 2. Проигрывает тот, кто делает последний ход.
б) То же самое, но в кучке 12 спичек.
в) То же самое, но в кучке 20 спичек, и можно брать от 1 до 4 спичек зараз.
г) (*) Сформулируйте общую стратегию игры, когда можно брать от 1 до k спичек. Решение

3. Остап Бендер провел сеанс одновременной игры в шахматы с двумя гроссмейстерами, причем с одним из соперников он играл чёрными фигурами, а с другим — белыми. За этот сеанс Остап получил 1 очко. (За победу в шахматной партии дается 1 очко, за ничью пол-очка, за поражение — 0 очков.) Как он смог этого добиться? Решение

4. а) Имеются две кучки по 10 спичек. Двое по очереди берут спички, причём за один ход разрешается брать любое количество спичек, но только из одной кучки. Проигрывает тот, кто не может сделать ход.
б) А если в одной кучке 20, а в другой 30 спичек?
в) Теперь у нас три кучки по 10 спичек. Двое по очереди берут спички, причём за один ход разрешается брать любое количество спичек, но только из одной кучки. Проигрывает тот, кто не может сделать ход. Решение

5. а) На шахматной доске в левом нижнем углу стоит фишка. В свой ход игрок может подвинуть её либо вправо на сколько угодно клеток, либо вверх на сколько угодно клеток. Проигрывает тот, кто не может сделать ход.
б) А если фишку можно двигать ещё и по диагонали вправо-вверх на сколько угодно клеток? Решение

6. В коробке 30 спичек. Двое по очереди берут из коробка не более половины лежащих в нём спичек (если пришла одна спичка, то берём её). Кто не может сделать ход — проиграл. У кого есть выигрышная стратегия? Какая? Решение

Рыцари и лжецы. Посидим за столом.

Мы приехали на остров, где живут два племени: рыцари, которые говорят правду и только правду, и лжецы, которые всегда лгут.

1. За столом по кругу сидит 12 аборигенов. Каждый из них говорит “Мой сосед справа — лжец”. Сколько среди них лжецов? Ответ

2. За столом по кругу сидит 10 аборигенов Каждый из них произнес фразу: «Следующие 4 человека, стоящие после меня по часовой стрелке, лжецы». Сколько среди них лжецов? Ответ

3. Вы опросили 1000 аборигенов, сидящих за огромным столом, и все они сказали: «Все остальные собравшиеся — лжецы». Сколько среди них рыцарей? Ответ

4. За столом сидят два жителя острова. Один из них сказал: ''По крайней мере, один из нас рыцарь''. Второй ему ответил: ''Ты лжец''. Кто из них кто? Ответ

5. Каждый из а) 7; б) 9 сидящих за круглым столом жителей острова сказал: ''Мои соседи лжец и рыцарь''. Сколько рыцарей и сколько лжецов сидит за столом? Ответ

6. В парламенте острова рыцарей и лжецов заседает 101 депутат. В целях сокращения бюджета на парламент руководство острова решило уменьшить состав парламента на одного человека. Но каждый из депутатов высказался, что если его исключат из парламента, то среди оставшихся депутатов большинство будут лжецами. Сколько лжецов и рыцарей было изначально в парламенте?Ответ

7. (*) Вы стоите на развилке двух дорог, одна из которых ведёт в аэропорт, но вы не знаете, какая. Какой вопрос вам надо задать прохожему, чтобы узнать, какая дорога ведёт в аэропорт?Ответ

8. (*) Вас поймали аборигены и хотят вас съесть. Они дают вам возможность выбрать свою судьбу: вы должны сказать одно утверждение, и если оно будет истинным, они вас пожарят с луком, а если ложным — потушат в сметане. Что надо сказать, чтобы остаться в живых? Ответ

АвиаКонструкции

1. В ряд выложены детали самолета, на которых написаны номера 7, 8, 9, 4, 5, 6, 1, 2, 3. За один ход разрешается взять несколько деталей, лежащих подряд, и переставить их в обратном порядке. Можно ли за три таких операции добиться расположения 1, 2, 3, 4, 5, 6, 7, 8, 9 и собрать самолет? Решение

2.  Летчик первого класса Кожедуб пробует завести мотор самолета. Для этого можно повернуть пропеллер на 7 или на 11 поворотов в любую сторону. Известно, что мотор может завестись при 15 поворотах по часовой стрелке. Как отмерить это летчику? Решение

3.  Командир сказал, что мы готовы к полету, помогите расставить багаж в багажном отсеке:
а) Разместите 3 коробки в три ряда по 2;
б) Разместите 8 сумок в четыре ряда по 3; где ряд – прямая линия.Решение

4. Среди четырёх летчиков нет трёх с одинаковым именем, или с одинаковым отчеством, или с одинаковой фамилией, но у каждых двух совпадает или имя, или отчество, или фамилия. Может ли такое быть? Решение

5. Радар представляет собой квадрат 8×8. В полете пилот может за один ход перейти на соседнюю по стороне клетку, после этого он должен перекрасить ее в противоположный цвет – белый либо синий. Сначала самолет стоит на угловой клетке и все клетки белые. Покажите, как можно оставить след на радаре в шахматном порядке. Решение

6. Самолеты приземляются на взлетную полосу, расположите 9 из них так, чтобы они образовали 10 прямых рядов по 3 самолета в каждом. 

7. На взлетной полосе с интервалом в один метр поставлены тысяча отметок. По этим отметкам прыгает кузнечик, который умеет прыгать только на 3 метки вперед или на 2 метки назад и больше никак. Как ему пропрыгать по всем отметкам, побывав на каждой ровно по одному разу? Решение

8. Найдите двузначный номер самолета, сумма цифр которого не меняется при умножении на любое однозначное число, кроме нуля. Решение

Геометрия

1. Деревянный кубик с ребром 3 см покрасили снаружи в красный цвет и разрезали на кубики с ребром 1 см.
а) Сколько получилось кубиков?
б) Сколько кубиков имеют одну красную грань?
в) Сколько кубиков имеют две красные грани?
г) Сколько кубиков имеют три красные грани?
д) Сколько кубиков не имеют ни одной красной грани? Ответ

2. Для окраски квадратного пола со стороной 4 м требуется 4 кг краски. Сколько краски потребуется для окраски квадратного пола со стороной 8 м? Ответ

3. После семи стирок и длина, и ширина, и высота кубического куска мыла уменьшились вдвое. На сколько стирок хватит оставшегося куска? Ответ

4. На глобусе провели 10 меридианов и 11 параллелей. Сколько кусков получилось? (Меридиан – это дуга от полюса до полюса, параллель – полный круг.) Ответ

5. Одну сторону прямоугольника уменьшили на 99 см, а другую увеличили на 1 см. Может ли площадь прямоугольника увеличиться? Ответ

6. Имеется три прямоугольных листа бумаги. Может ли так быть, что никакими двумя из них нельзя полностью накрыть третий? Ответ

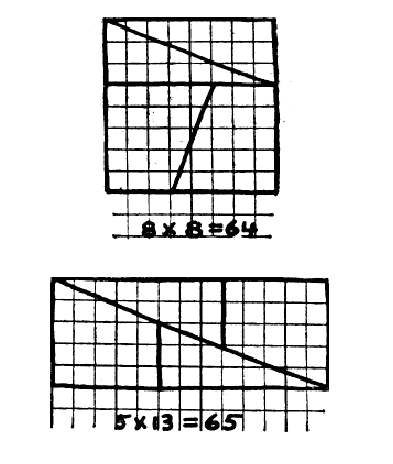
7. Квадрат 8 на 8 (площадь равна 64) разрезали на 4 части и из них сложили прямоугольник 5 на 13 (площадь равна 65). Получается, 64 равно 65? Найдите ошибку!

Объяснение

8. От каждой вершины деревянного куба отпилили по одинаковому кусочку так, что место спила имеет форму треугольника. Сколько вершин и сколько ребер у получившегося тела? Ответ

9. Грань куба разделена на 4 равных квадрата, и каждый квадрат окрашен в один из трех цветов: красный, синий и зеленый так, что квадраты, имеющие общую сторону, окрашены в разные цвета. Сколько может быть красных квадратов? Решение перебором не принимается. Решение Ответ

Взвешивания

Во всех задачах мы пользуемся чашечными весами. Если специально не указано, то у нас нет даже гирь!

0. Имеются чашечные весы и три монеты. Одна из монет фальшивая, она легче остальных. Как за одно взвешивание определить фальшивую монету? Решение

1. а) Перед вами 9 монет, одна из них фальшивая (легче настоящих). Как за два взвешивания выяснить, какая монета фальшивая?
б) Перед вами 81 монета, одна из них фальшивая (легче настоящих). Сколько взвешиваний понадобится, чтобы выяснить, какая монета фальшивая?
в) А если монет 10, сколько взвешиваний понадобится? Решение

2. Есть три монеты, одна из них фальшивая (но нам неизвестно, легче она или тяжелее, чем настоящие). Как выяснить, какая монета фальшивая? Обойдитесь как можно меньшим количеством взвешиваний. Решение

3. Как при помощи чашечных весов без гирь разделить 24 кг гвоздей на две части — 9 и 15 кг? Решение

4. Лиса Алиса и Кот Базилио — фальшивомонетчики. Базилио делает монеты тяжелее настоящих, а Алиса — легче. У Буратино есть 15 одинаковых по внешнему виду монет, но какая-то одна — фальшивая. Как двумя взвешиваниями на чашечных весах без гирь Буратино может определить, кто сделал фальшивую монету — Кот Базилио или Лиса Алиса? (Находить монету не надо.) Решение

5. Из пяти монет две фальшивые. Одна из фальшивых монет легче настоящей, а другая — на столько же тяжелее настоящей.Объясните, как за три взвешивания на чашечных весах без гирь найти обе фальшивые монеты. Решение

6.  Золотоискатель добыл 9 кг песка. Ему надо отмерить 2 кг песка с помощью весов с двумя чашами и одной гирей — 200 г. Как это сделать за 3 взвешивания? Если мы добиваемся равновесия путем пересыпания песка — это одно взвешивание. Есть пакеты для хранения песка. Решение

7. Семь монет расположены по кругу. Известно, что какие-то четыре из них, идущие подряд, — фальшивые и что каждая фальшивая монета легче настоящей. Объясните, как найти две фальшивые монеты за одно взвешивание на чашечных весах без гирь. (Все фальшивые монеты весят одинаково.) Решение

8. Дан мешок сахарной пудры, чашечные весы и гирька в 1 г. Как за 5 взвешиваний отмерить 31 г сахарной пудры? Решение

9. В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать суммарный вес любых двух яблок. Придумайте способ выяснить за 8 взвешиваний суммарный вес всех яблок. Решение

Алгоритмы

0. Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям?

0.Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда: 5-литровый и 7-литровый. Как ему это сделать?

1.Трое учеников пошли на рыбалку, взяв с собой лодку, выдерживающую нагрузку до 100 кг. Как перебраться ученикам с берега реки на остров, если их массы равны 40 кг, 50 кг, 70 кг?

2. В подвале лаборатории растут мандрагоры и имеется неограниченный запас мандрагорового экстракта. Как при помощи мензурок объёмом 5 и 7 миллилитров отмерить 4 миллилитра мандрагорового экстракта? Но берегитесь! Если ни на одном из этапов ни в одной из мензурок не окажется ровно 3 миллилитра экстракта, мандрагоры закатят истерику и криками разрушат лабораторию! Решение

3. К реке, у берега которой находилась лодка, вмещающая только двух человек, подошли два разбойника и два путешественника. Разбойники не решались напасть на путешественников. Они могли бы совершить нападение, только если на берегу остались бы два разбойника и один путешественник. У одного из разбойников была сломана рука, и он даже не мог грести веслами. Как надо переправиться через реку разбойникам и путешественникам, чтобы последние избежали нападения?

4. На камнях сидит шесть лягушек (как на картинке). Лягушки-мальчики хотят пересесть на камни, где сидят лягушки-девочки, а лягушки-девочки хотят пересесть на камни, где сидят лягушки-мальчики. Каждая лягушка может прыгнуть либо на соседний камень (если он свободен), либо перепрыгнуть на камень сразу за соседней лягушкой (если он свободен). Как лягушкам поменяться местами?


5. Решите предыдущую задачу при дополнительном условии: лягушки не могут прыгать назад, только вперёд! Эту задачу можно решать, например,  вот тут.

6. Шли два маляра, навстречу — еще двое. У каждого руки испачканы своей краской, и никому не хочется пачкаться чужой. Маляры хотят поздороваться друг с другом (каждый из первой пары с каждым из второй и наоборот) рукопожатием, но на всех есть только две перчатки. Как им можно решить эту проблему? Перчатки не выворачиваются. Решение

7. Семья супергероев ночью подошла к мосту. Бабушка-Молния может перейти его за 1 минуту, Железный Малыш — за 2 минуты, Криптонитовая Мама — за 5 минут, а Папа-Енот — за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей из их скоростей. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя. Летать нельзя.) Решение

8. Есть 10-этажное здание. Есть обезьянка. У обезьянки есть два кокоса. Она может залезть на любой этаж и скинуть один кокос. Если этаж высокий – кокос разобьется и его нельзя будет больше кидать. Как, потратив не больше 4 бросков, гарантированно установить, начиная с какого этажа кокосы начинают разбиваться? Решение

9. У императора Палпатина работает 10 сотрудников. Каждый месяц император повышает зарплату на 1 рубль ровно девятерым (по своему выбору). Как Палпатину повышать зарплаты, чтобы сделать их одинаковыми? (Зарплата - целое число рублей.) Решение

10.  Неуловимый Джо никогда не проигрывает на рулетке больше четырех раз подряд и никогда не ставит больше 10 долларов. Как ему выиграть 1000 долларов? (В случае выигрыша на рулетке возвращается удвоенная ставка; вначале Джо имеет 100 долларов.) Решение

Криптография

Шифр Цезаря - это вид шифра замены, в котором каждая буква заменяется буквой, находящейся на некотором числе позиций правее неё в алфавите. Например, в шифре со сдвигом на 3, А была бы заменена на Г, Б станет Д, и так далее. Алфавит считается записанным по кругу; так, в приведённом примере буква Ю переходит в Б. Число, на которое мы сдвигаем, называется ключом шифра.

Шифр Виженера - усовершенствованный вариант шифра Цезаря. У нас есть ключевое слово, например, БАНК. Мы заменяем каждую его букву на её номер в алфавите: 2 1 15 12. Затем к буквам слова, которое хотим зашифровать, прибавляем по одной числа ключевой последовательности (если она закончилась, начинаем заново). Например, если мы хотим зашифровать слово ГВАРДИЯ, то получим: Г + 2 = Е, В + 1 = Г, А + 15 = О, Р + 12 = Ь, Д + 2 = Ё, И + 1 = Й, Я + 15 = М. Получили ЕГОЬЁЙМ.

1. Напишите, как зовут ваших лучших друзей. Зашифруйте их имена шифром Цезаря с ключом 1 и дайте преподавателям расшифровать.

2. Используя шифр Цезаря с ключом 1, расшифруйте. О ком это сказано? ПО ГТЁДЕБ ВЬМ ОЁ РСПШЭ РПЕЛСЁРЙУЭТА. ЛСПНЁ УПДП, ПО ВЬМ РПЮУ. Ответ

3.  Г ОЦЪЫЗ ЖГЕГМ РГСДСУСХ - 8 ТЛУСЁСЕ Л СЖРГ ФЕЗЪНГ. (ключ 3, шифр Цезаря) Ответ

4. Здесь нужно подобрать ключ для шифра Цезаря. ФЖ ЦТЖФЛЩЛ СХФШЛЧИФВЬ ЗЖФХС ЗЖФСП ЦХКЧЖТПШГ Ш ЩЪЯМФСХР! Ответ

5. Зашифруйте шифром Виженера с ключом «ШИФР» слово «АНАНАС». Ответ

6. Слово ЗЁВЭОЖЭ получено с помощью шифра Виженера с ключевым словом ЧАЙ. Восстановите исходное слово. Ответ

7. (*) Внимание! В этой задаче в алфавите нет букв ё, й, ъ! Сообщение (из нескольких слов) зашифровано шифром Виженера. Известно, кто ключевая последовательность букв не содержала никаких букв, кроме А, Б и В. Прочтите шифрованное сообщение: РБЬНПТСИТСРРЕЗОХ Ответ

 Ещё 19 задач

1. Первая цифра пятизначного числа равна количеству нулей в этом числе. Вторая цифра – количеству единиц (цифр „1”) в этом числе. Третья цифра – количеству двоек, четвертая – количеству троек, пятая — количеству четвёрок. Придумайте такое число. Ответ

2. Десять джедаев съедают двадцать пицц за двадцать минут. Сколько пицц съедят двадцать джедаев за час? Ответ

3. Цифрами 0, 1, 2, 3 запишите наибольшее шестизначное число. (Каждую цифру надо использовать хотя бы один раз.) Ответ

4. Аня задумала число. Она прибавила к нему 5, разделила сумму на 3 и получила 2. Какое число задумала Аня? Ответ

5. Надя на 5 лет старше Феди. Сколько лет будет Наде через год, если год назад им вместе было 17? Ответ

6. Аня отметила на прямой 10 точек. Затем в каждый промежуток между точками она поставила еще по точке. Потом в каждый новый промежуток – еще по точке. Сколько точек отмечено в итоге? Ответ

7. Масса ящика с апельсинами равна 35 кг. После продажи половины всех апельсинов ящик поставили на весы. Весы показали 21 кг. Какова масса пустого ящика? Ответ

8. Человек понял, что он может выложить пол комнаты, имеющий квадратную форму, квадратной плиткой, и что ему не понадобится ни одну из них разрезать. Он положил 28 плиток по краям комнаты. Сколько всего ему понадобится плиток, чтобы покрыть весь пол? Ответ

9. Маленький коала съедает листья с одного эвкалиптового дерева за 10 часов, а каждый из его родителей ест вдвое быстрее. За сколько времени это семейство объест все листья с одного эвкалиптового дерева? Ответ

10. Коля, Вася и Боря играли в шашки. Каждый из них сыграл всего 2 партии. Сколько всего партий было сыграно? Ответ

11. На доске написали числа 51, 52, ...., 101. Сколько чисел написали на доске? Ответ

12. У Насти и Ани денег поровну. Сколько денег должна дать одна из них другой, чтобы у Насти стало на 10 рублей больше, чем у Ани? Ответ

13. В шкафу есть 2 шляпы, 3 плаща и 5 шарфов. Сколькими способами можно одеться? Ответ

14. Какое слово зашифровано: 1762561564? Каждая буква заменена своим номером в алфавите. Ответ

15. Разрежьте прямоугольник 6×9 на 8 квадратов.

16. Чтобы получить 9 стаканов Работомозгоулучшательного Зелья, нужно 2 стакана вороньих перьев, 3 стакана экстракта слизней, 1 стакан ресниц дракона и 3 стакана воды. Сколько нужно взять литров экстракта слизней, чтобы получить 21 литр Работомозгоулучшательного Зелья? Ответ

17. Если для вчера завтра был четверг, то какой день будет вчера для послезавтра? Ответ

18. В семье есть Иван Сидорович, Сидор Иванович, Сидор Петрович, Петр Сидорович, Петр Петрович. Один из них сейчас смотрит телевизор, его отец дремлет, брат читает газету, а дети ушли гулять. Как зовут того, кто смотрит телевизор? Ответ

19. В оранжерее были срезаны гвоздики: белых и розовых - 400 штук, розовых и красных - 300, белых и красных - 440. Сколько гвоздик каждого цвета было срезано в оранжерее? Ответ