Математика 5 класс
facebook vk
Локация Главная страница Карта сайта
Математика - это интересно! Математика - это здорово!
Задача 1. Знакомимся с высказываниями
Вруниш (всегда говорит неправду) и Правдиш (всегда говорит правду) решили взять для внука одного кота: рыжего, белого или черного.
Правдиш: Рыжего брать не будем.
Вруниш: Возьмём белого.
Определи, кого же они выбрали.
Правдиш всегда говорит правду. Значит, рыжего кота брать не будут.
Вруниш всегда говорит неправду. Добавь к его высказыванию "НЕ" и посмотри, что получится.
Правдиш говорит правду. Значит, кот-везунчик НЕ рыжий.
Вруниш всегда говорит неправду. Значит, домой возьмут НЕ белого кота.
НЕ рыжий и НЕ белый, значит, чёрный.
Ответ: чёрный.
Задача 2. Последовательное исключение вариантов
Вика, Полина и Коля раскрашивали картинки карандашами трёх цветов: красным,синим и зелёным.
Вика раскрашивала НЕ красным и НЕ синим.
Коля – НЕ синим.
Какой карандаш был у каждого ребёнка?
Вика раскрашивала НЕ красным и НЕ синим.
Подумай, карандашом какого цвета она рисовала?
Ответ: у Вики был зелёный карандаш, у Полины - синий, у Коли - красный.
Задача 3. Думай частями от целого
По правилам пользования, грузовой лифт в гостинице вмещает и может перевезти не более 15 взрослых или не более 20 детей.
Какое наибольшее число детей может ехать в лифте с шестью взрослыми?
Есть некоторая максимальная масса груза, которую может безопасно перевозить лифт.
Этот максимум - масса 15 взрослых человек или масса 20 детей.
Пятая часть этого максимального груза - это трое взрослых или четверо детей.
Максимальный груз, который может безопасно перевозить лифт - 15 взрослых или 20 детей. Пятая часть этого максимального груза - это трое взрослых или четверо детей.
Если в лифт зайдут 6 взрослых (две части от общей допустимой массы), дети могут дополнить три оставшиеся части:
4 ∙ 3 = 12.
Ответ: 12.
Задача 4. Разбираем, рассуждаем
Егор, Иван и Сергей – друзья. У них разные увлечения: один пишет стихи, второй играет в футбол, а третий - шахматист.
Как-то один из них сообщил другому: «Иван, мы обыграли соперника со счетом 2:1. Я смог отразить все пенальти!».
Иван тут же отправил их товарищу sms такого содержания: «Сергей, срочно придумай стишок о победе наших футболистов».
Догадайся, как зовут футболиста.
Эту задачу можно решать с помощью таблицы или путем последовательных рассуждений.
Первое сообщение про победу адресовано Ивану, это означает, что он не футболист. Из следующего условия задачи понятно, что стихи пишет Сергей. Значит, в футбол играет Егор.
Ответ: Егор.
Ответь на вопросы и получи оценку
Повторение курса математики 4 класса
5 класс Карточка 0-1
1.Вырази в часах и минутах 67 мин, 200 мин.
2.Вырази в сотнях и десятках 27 десятков.
3.Дополни предложение: «При умножении нуля на число получается …»
4.Двум мальчикам и трем девочкам раздали 15 вишен поровну каждому. Сколько вишен получили мальчики? Сколько вишен получили девочки?
5.Сколько цифр будет в частном при делении 24 684 на число 2?
6.Вычисли устно 3030:3, 42042:7.
7.Какие остатки могут получиться при делении на число 8?
8.Закончи предложение: «Если нуль разделить на число, не равное нулю, то получится…»
9.Закончи предложение: «Окружность – это граница…»
10.Расставьте в записи 7 · 9 + 12 : 3 – 2 скобки так, чтобы значение получившегося выражения было равно 23.
1.1.Натуральные числа и нуль. Натуральный ряд
5класс Карточка 1-1
1-6 на с. 6.
7. № 1.61 (2) на с. 52.
8. № 1.62 (1) на с. 52.
9. № 1.63 (2) на с. 52.
10.Меры длины на форзаце
5 класс Карточка 1-2
1-6 на с. 6.
7. № 1.61 (4) на с. 52.
8. № 1.62 (3) на с. 52.
9. № 1.63 (4) на с. 52.
10.Меры массы на форзаце
1.2. Точка, прямая, плоскость
5 класс Карточка 2-1
1-3 на с. 6.
4. № 1.64 (1) на с. 52.
5. № 1.65 (2) на с. 53.
6. № 1.24 (1) на с. 12.
7.Как умножить число 4 на 10, на 100, на 1000?
8.Какой порядок выполнения действий в выражениях без скобок?
9.Как найти неизвестное слагаемое в уравнениях х + 3 = 5 , 3 + х = 5?
10.Как найти неизвестное уменьшаемое в уравнении х – 4 = 2 и неизвестное вычитаемое в уравнении 9 – х = 7?
5 класс Карточка 2-1
1-3 на с. 6.
4. № 1.64 (3) на с. 52.
5. № 1.65 (4) на с. 53.
6. № 1.24 (2) на с. 12.
7.Как разделить число 7000 на 10, на 100, на 1000?
8.Какой порядок выполнения действий в выражениях со скобками?
9.Как найти неизвестный множитель в уравнениях х ·3 = 12 , 3 · х = 12?
10.Как найти неизвестное делимое в уравнении х : 2 = 3 и неизвестный делитель в уравнении 8: х = 2?

Десять полезных советов для тех, кто хочет подружиться с математикой
1.Настройтесь на успех.
Если ты достаточно успешно справляешься с другими школьными дисциплинами, ты просто не можешь не справиться с математикой - это только дело времени и твоего собственного труда. При изучении математики используются те же логические построения, что и в остальных науках, поэтому нет ничего удивительного в том, что великий математик Бертран Рассел был также и философом, а многие известные музыканты - математиками.
2.Постоянно тренируйтесь.
Окружающий нас мир полон множеством чисел, которыми мы постоянно пользуемся. Почему бы не попробовать использовать их для тренировки наших математических способностей и начать складывать числа на номерах проезжающих мимо машин, считать количество шагов до школы, магазина и узнавать скорость нашего движения до этих пунктов?
3.Воспринимайте математические примеры как игру.
Самый сложный и страшный пример попробуйте превратить в игру, а все возможные варианты его решения, пусть даже сначала ошибочные, воспринимайте как захватывающую погоню за кладом. Все пройденные правила и теоремы надо знать наизусть, никаких пробелов быть не должно - именно они основа всего, без них не обойтись так же, как и без знания карты местности, где зарыт клад.
4.Необходимо хорошо понимать смысл правил и теорем.
Вы не сдвинетесь с места, если будете просто зазубривать все теоремы. Необходимо очень хорошо представлять себе, о чем именно в ней идет речь. Вам мало поможет тот факт, что "квадрат гипотенузы равен сумме квадратов катетов", если вы не очень представляете, что такое катет и где он находится.Во время объяснения учителем нового материала не стесняйтесь спрашивать сразу, что непонятно, поскольку именно для этого учитель и находится в классе.
5.Создайте себе окружение из формул.
Окружи себя формулами, которые тебе необходимо выучить. Напиши их на листе бумаги и повесь в своей комнате или около зеркала в ванной. Постоянно натыкаясь на них, ты запомнишь их как навязчивую телевизионную рекламу и, в случае надобности, всегда сможешь вызвать их в памяти.
6.Не ломайте голову в одиночестве!
Длинные тоскливые примеры и сложнейшие задачи прямо-таки преображаются, оживают, если к их решениям приступить в компании с другом или подругой. Обмениваясь каждый своим вариантом решения, легче и веселее идти к истинному ответу.
7.Внимательно читайте задание.
Очень часто ключ к решению задачи таится в ее условии, и все ваши неудачи из-за того, что вы невнимательно прочитали задание. Внимательно и вдумчиво прочитайте задание и только потом приступайте к решению!
8.Действуйте методически.
Прежде всего исходите из данных, имеющихся в вашем распоряжении, изобразите их все при помощи таблиц или чертежей на листе бумаги для наглядности. Воспроизведите в памяти и напишите все теоремы или правила, вам известные и имеющие отношение к данному вопросу.
9.Постоянно контролируйте свои действия.
Каждый раз проверяйте все произведенные математические операции, чтобы в них не закралась какая-нибудь неточность, которая потом повлияет на правильность окончательного решения. Также не забывайте проверять, все ли исходные данные были вами задействованы - они не могут остаться невостребованными в решении задания.
10. Наведите порядок в цифрах.
Математика - наука точная, и, как ни одна другая, не терпит даже малейших неточностей. Сколько уже вы наделали ошибок из-за неправильно прочитанного числа, лишнего нуля или если пишете "как курица лапой".
Человек подобен дроби: числитель - то, что он есть, знаменатель - то, что он о себе думает. Чем больше знаменатель, тем меньше дробь". Лев Николаевич Толстой.
А-р-и-ф-м-е-т-и-к-а – любовь на всю жизнь( воспоминания детского врача Кати Брехман, письмо приведено без изменений) |
| Уважаемые друзья арифметики ! Обстоятельства места и времени: 1947-48 гг. Ташкент, окраина, полу-сельская местность, школа-семилетка, 5-й Класс. Это моя третья школа. Мне 13 лет. В нашем 5-А классе 35-38 разновозрастных учеников. Ранние послевоенные годы.Арифметику преподает немолодая Учительница, в прошлом преподаватель гимназии. Возможно из репрессированных и отправленных в Узбекистан еще до войны. Это мои домыслы, т.к. она очень выгодно выделялась среди других учителей внешним видом, красивой русской речью, культурой общения с детьми и коллегами. Точно помню, что у Учительницы были проблемы с передвижением, поэтому в школу и из школы ее всегда сопровождали ученики нашей школы, вели под руку, несли портфель. Подготовка класса к уроку. Во время перемены два дежурных готовили класс к уроку. Большая длинная доска начисто вытерта, разделена на 4 части. Стол Учительницы стоит у наружной стены класса, а не в центре. Звонок, Учительница входит, все встают, она проходит к своему столу. Здоровается, садится. Выходят два дежурных и становятся перед Учительницей. Начало урока. Учительница: Здравствуйте, дети, садитесь! Ученики: 1-й дежурный: Класс к уроку готов! Доска разделена на 4 части, имеется 4 мела и 4 тряпки. 2-й дежурный: В классе по списку 35 человек. Присутствуют все! Домашнее задание выполнили все. Варианты: В классе отсутствует Иванов - болен. Домашнее задание не выполнили Петров и Сидоров. или: В классе отсутствует Иванов, первый день, по неизвестной причине. (Если отсутствует второй день, то причина уже должна быть известна!). Учительница: Хорошо, садитесь. К доске идут Соколова, Жемчугова, Ким и Койфман (это - я). Вызванные ученики идут к доске, проходя мимо стола Учительницы, получают задание на листочках, каждый идет к своему участку на доске и приступает к выполнению задания. Задания имеют своей целью проверить, как усвоен пройденный материал. Учительница: Ко мне идут Жарова, Соболева, Коник, Боров. Каждый получает на листочке задание для устного счета. Они становятся лицом к Учителю, в линеечку и по очереди отвечают, без предварительной подготовки. Весь класс слушает и оценивает ответы товарищей. Все 4 ответа и их обсуждение занимает 10-15 минут. Ученики идут на место. За это время готовы к ответу ученики у доски. Обсуждение и оценка ответов идет в таком же порядке (еще 10 минут). Дальнейшая часть урока отводится объяснению нового материала и его закреплению. Иногда с целью закрепления и проверки усвоения очень быстро каждому раздавались небольшие листочки-"летучки" с заданием и каждый решал в своей тетради. Домашнее задание давалось в конце урока: Учительница писала на доске страницы и номера задач и примеров. Если было сложное домашнее задание и большинство не справилось, то урок начинался с пояснений к этому заданию. При этом один из тех, кто справился, выходил к доске и объяснял всему классу. (Если ребенок решил сам, то он мог объяснить, а если нет, то значит списал, либо кто-то помогал ему решать, не объяснив процесса решения). О правилах и терминах. Очень большое внимание уделялось изучению правил: они были четкие, лаконичные, понятные, заносились в тетради и брались в "рамочки". Нас учили свободно оперировать математическими терминами: слагаемое, множитель, делимое, делитель, частное, др. О тетрадях. Несмотря на кризисную ситуацию с бумагой в военные и первые послевоенные годы, каждый имел на целый год 4 толстые тетради (по количеству четвертей), одна тетрадь для контрольных работ на весь год. Кроме того, в классе была Классная круговая тетрадь. На первой странице этой тетради был написан список учеников класса (как в классном журнале). Каждый день эта тетрадь передавалась по списку следующему ученику, и она у него была сутки. Ученик в этот день не пользуется своей тетрадью, а все, что пишется в классе и домашнее задание, он выполняет в этой тетради. В день контрольной работы, последняя решалась тем учеником, у кого была тетрадь в этот день. Один раз в неделю тетрадь бралась для проверки. В течение четверти ученик получал достаточное количество оценок, что давало возможность без труда объективно оценить каждого. Дисциплина была прекрасная, класс был дружный и особо отстающих тоже не было. Я не помню, чтобы кто-то из моих соучеников неуважительно относился к нашей Учительнице, проявлял какое-то недовольство или осуждение в ее адрес. Последствия. В начале второй четверти 6 класса (1948) я с родителями вернулась в г. Винницу, УССР, откуда эвакуировались в июне 1941 г. Я продолжила учебу в 6-м классе, который был переполнен: по 3 человека на одной парте. По школьной программе я опережала своих новых соучеников в изучении арифметики, что давало мне определенные преимущества. Новый, умный учитель арифметики, бывший фронтовик, в военном кителе сразу обратил на меня внимание и почти ежедневно спрашивал и с места и у доски. Особенно его интересовало знание правил. Положение его было не простое (это я уже сейчас понимаю). Он, по сути, "учился" у меня, не подавая вида перед остальными учениками. Я сразу же завоевала авторитет в классе. Это была единственная в городе смешанная (железнодорожная) школа, а половина класса еврейские ребята. Конечно, у меня была куча проблем с украинским и отчасти с русским языками (я фактически не училась в первом классе - условия жизни в эвакуации). Но Арифметика, моя спасительница, определила мне достойное место в новой, четвертой в моей жизни школе. Ни одна из других математических дисциплин - алгебра, геометрия, тригонометрия - не стала для меня такой близкой и значимой как Арифметика. Уважаемые Игорь и Эстер, если вы дочитали до этой последней строчки, то я благодарю вас за терпение и за то, что я с помощью этого письма вспомнила УЧИТЕЛЬНИЦУ, которая заслуживает, чтобы ее помнили около 60 лет. С уважением Катя Брехман. |
Лист самоконтроля 12 (5 класс)
1.Как сложить дроби с разными знаменателями?(Вопрос 1 на ст.122)
2.Чему равна разность дробей с одинаковыми знаменателями?(Вопрос 1 на ст.132)
3.Чему равно произведение двух дробей?(Вопрос 1 на ст.147)
4.Сформулируйте распределительный закон умножения относительно вычитания. (Вопрос 2 на ст.159)
5.Сформулируйте основное свойство частного. (Вопрос 5 на ст.170)
6. Как найти, какую часть составляет число а от числаb?(Вопрос 1 на ст.178)
7.Известно, что задании е выполняется за n часов. Какая часть задания будет выполнена: а) за 1 ч; б) за 2 ч; в) за k часов? (Вопрос на ст.184)
8.Как представить смешанную дробь в виде неправильной дроби? (Вопрос 5 на ст.192)
9.Между какими последовательными натуральными числами заключена смешанная дробь? (Вопрос 2 на ст.197)
10.Что значит выражение «точка М с координатой 1 и 2/3»?(Вопрос 2 на ст.201)
11.Как вычисляется разность смешанных дробей, когда дробная часть уменьшаемого: а) больше или равна дробной части вычитаемого; б) меньше дробной части вычитаемого? (Вопрос на ст.212)
12.Как найти частное смешанных дробей?(Вопрос 2 на ст.218)
13. Чему равны квадраты чисел 11, 12, 13, 14, 15, 16, 17, 18, 19? (Левый форзац)
14.Запишите формулу для вычисления периметра Р прямоугольника с измерениями а и b. Запишите формулу для вычисления площади S прямоугольника с длинами сторон а и b. (Ст. 46).
15.Какие прямые называются перпендикулярными? (Вопрос 2 на ст.40)
Лист самоконтроля 13 (5 класс)
1.Как найти разность дробей с разными знаменателями?(Вопрос 1 на ст.136)
2.Как формулируется распределительный закон умножения относительно сложения?(Вопрос 1 на ст.159)
3.Какие два числа называются взаимно обратными? (Вопрос 1 на ст.164)
4.Как разделить дробь на дробь? (Вопрос 4 на ст.170)
5.Как найти часть от числа, если часть выражена дробью?(Вопрос 2 на ст.178)
6.Как найти число по части от него, выраженной дробью?(Вопрос 3 на ст.178)
7.Как найти целую и дробную части неправильной дроби? (Вопрос 1 на ст.191)
8. как сравнить смешанные дроби: а) с разными целыми частями; б) с одинаковыми целыми частями? (Вопрос 1 на ст.197)
9.Как на координатном луче изобразить числа 1/3, 2/3, 7/3, 1и 2/3, 2 и 1/3? (Вопрос 1 на ст.201)
10.Как сложить смешанные дроби? (Вопрос на ст.206)
11.Как умножить смешанные дроби? (Вопрос 1 на ст.218)
12.Что называется средним арифметическим нескольких чисел? (Вопрос на ст.226)
13.Чему равны кубы чисел 1, 2, 3, 4, 5, 6, 7, 8, 9? (Левый форзац)
14.Запишите формулу для вычисления периметра Р квадрата с длиной стороны а. Запишите формулу для вычисления площади S квадрата с длиной стороны а.
15.Какое свойство смежных углов вы знаете? (Вопрос 4 на ст.18)
Карта сокровищ.Всероссийский математический конкурс
Олимпиада по математике (5 класс)
Как нет на свете без ножек столов,
Как нет на свете без рожек козлов,
Котов без усов и без панцирей раков,
Так нет в математике действий без знаков.
Папа у Васи силен в математике
Папа у Васи силен в математике,
Учится папа за Васю весь год,
Где это видано, где это слыхано,
Папа решает, а Вася сдает?
Лист самоконтроля 10 (5 класс)
1.Какое число называется простым? Составным? (Вопрос 1 на ст.4)
2.Чему равен развернутый угол? Прямой угол? (Вопрос 2 на ст.18)
3.Какое свойство смежных углов вы знаете? (Вопрос 4 на ст.18)
4.Как найти НОД двух (нескольких) чисел? (Вопрос 3 на ст.28)
5. Запишите формулами:
а) переместительный и сочетательный законы сложения и умножения;
б) распределительный закон умножения относительно сложения и относительно вычитания. (Вопрос 1 на ст.47)
6.Два пешехода движутся по одной и той же дороге со скоростями а км/ч и b км/ч (абольше b). В каком направлении они движутся по отношению друг к другу, если скорость (в км/ч) их сближения равна: а) а +b; б) а –b? Через какое время встретятся пешеходы, если до начала движения расстояние между ними было sкм? (Вопрос 2 на ст.53)
7.Что называется знаменателем дроби? Числителем дроби? (Вопрос 2 на ст.62)
8.Как можно записать частное от деления одного натурального числа на другое (например, а на b)? (Вопрос 1 на ст.67)
9.Как найти, какую часть составляет число k от числа n? Какой дробью выражается часть, которую составляет: а) число 5 от числа 7; б) число а от числа b? (Вопрос 1,2 на ст.70)
10.Как найти число по части от него? Как найти число, если 2/3 от него равны: а) 40; б) p? (Вопрос 1,2 на ст.80)
11.Что значит сократить дробь? (Вопрос 1 на ст.94)
12.Как сравнить две дроби с одинаковыми знаменателями? (Вопрос 1 на ст.106)
13.Какая дробь называется правильной? Неправильной? (Вопрос 1 на ст.111)
Лист самоконтроля 11 (5 класс)
1.Что значит: разложить число на простые множители? (Вопрос 1 на ст.8)
2.Какой угол называется острым? Тупым? (Вопрос 3 на ст.18)
3.Какое число называется общим делителем двух чисел? (Вопрос 1 на ст.23)
4.Как найти наименьшее кратное двух (нескольких) чисел? (Вопрос 3 на ст.35)
5.Какие прямые называются перпендикулярными? (Вопрос 2 на ст.40)
6. Запишите известные вам формулы для вычисления площадей и объемов геометрических фигур. (Вопрос 2 на ст.47)
7. Два пешехода движутся по одной и той же дороге со скоростями а км/ч и b км/ч (а больше b). В каком направлении они движутся по отношению друг к другу, если скорость (в км/ч) их сближения равна: а) а +b; б) а –b? Чему равно расстояние между пешеходами до начала движения, если они встретились через t ч? (Вопрос 3 на ст.53)
8.Что показывает знаменатель дроби? Числитель дроби? (Вопрос 3 на ст.62)
9.Как найти часть (дробь) от числа? Как найти часть от числа 15, если она выражена дробью: а) 2/3; б) p/q? (Вопрос 1,2 на ст.74)
10.Сформулируйте основное свойство дроби. (Вопрос 1 на ст.88)
11.Как можно привести дроби к общему знаменателю? (Вопрос 3 на ст.101)
12.Как можно сравнить две дроби с разными знаменателями? (Вопрос 2 на ст.106)
13.Чему равна сумма дробей с одинаковыми знаменателями? (Вопрос 1 на ст.119)
С помощью 4 и 7-литровых сосудов набрать 6 л воды
Занимательные задачи по математике
Упражнения и задачи по математике.
Игра для развития логического мышления
Интерактивная
книжечка "Сократ":
Понравилась эта книжечка и Вы
хотите послать ее
к себе на почту? Онлайн тесты по математике
Олимпиада по математике для 5-6 классов
23-25.01.2014 года. 2-й этап дистанционной олимпиады по математике Гродненского университета.
5 класс
1. Для числа 345 укажите числа, на которые оно делится.
Ответ 1 5
Ответ 2 7
Ответ 3 3
Ответ 4 2
Ответ 5 23
2.Мама, Андрей и Рита вместе идут в детский сад. За то время, пока мама делает 2 шага, Андрей делает 3 шага, а пока Андрей делает 2 шага, Рита делает 3 шага. Сколько шагов прошла мама, если Андрей и Рита вместе сделали 240 шагов?
Решение.
За то время, пока мама делает 4 шага, Андрей делает 6 шагов, Рита – 9, а Андрей и Рита вместе – 15. Имеем: 4 шага мамы – 15 шагов Андрея и Риты;
х шагов мамы – 240 шагов Андрея и Риты.
х = (4·240):15 = 64.
Ответ: 64 шага.
3. Округлите число 20142301 до тысяч. В ответ запишите округленное число.
4. Семья состоит из четырёх человек: мамы, папы, сына и дочери. Папа на 3 года старше мамы. Мама в 4 раза старше сына и в 3 раз старше дочери. Сколько лет дочери, если сумма возрастов всех членов семьи 96 лет?
Ответ: 12 лет.
5. В одной семье было много детей. 8 из них любили конфеты, 5 - печенье, 7 - торты, 3 - конфеты и печенье, 4 - конфеты и торты, 2 - печенье и торты, один - и конфеты, и печенье, и торты. Сколько детей было в семье?
Решение.
Если изобразить множества детей-любителей конфет, печенья и тортов в виде трех пересекающихся кругов, то число детей равно 8+7+5-3-4-1-1= 11.
Ответ: 11.
6. Петя перемножил все числа от 1 до 15. Сколькими нулями оканчивается получившееся число?
Ответ: 3.
7. Сколько секунд в двух сутках?
Ответ 1 43200
Ответ 2 3600
Ответ 3 86400
Ответ 4 172800
Ответ 5 24000000
8. Леша задумал число, умножил его на 40, затем задуманное число умножил на 66 и результаты сложил. В сумме он получил число 2014. Какое число задумал Леша?
Ответ:19.
9. Андрей задумал трехзначное число, у которого с любым из чисел 728, 129 и 794 совпадает один из разрядов, а два других не совпадают. Какое число задумал Андрей?
Ответ: 198.
10. Выберите, какими цифрами может оканчиваться квадрат натурального числа
Ответ 1 1
Ответ 2 2
Ответ 3 3
Ответ 4 4
Ответ 5 5
Ответ 6 6
Ответ 7 7
Ответ 8 8
Ответ 9 9
Ответ 10 0
11. На дистанционной олимпиаде по математике Школы точных наук в 5 классе участникам предложили 25 задач. За правильный ответ ученику ставили 10 баллов, а за неправильный списывали 8 очков. Сколько правильных ответов дал один из учеников, если он ответил на все вопросы и набрал 88 очков?
Ответ:16.
12. Андрей и Саша на велосипедах выехали одновременно навстречу друг другу из Гродно и Щучина. Скорость Андрея 10 км/ч, скорость Саши 11 км/ч. Какое расстояние будет между мальчиками через 2 часа, если расстояние от Гродно до Щучина 67 км? Ответ запишите в километрах.
Ответ: 25.
Как быстро считать в уме — несколько простых приемов для сложных повседневных вычислений в голове
Этот список нескольких малоизвестных математических трюков покажет вам как быстро считать в уме в случаях, посложнее чем 5 умножить на 10, а ещё ваши знакомые смогут пользоваться вами, как калькулятором.
1. Умножаем на 11
Все мы знаем, как быстро умножить число на 10, нужно лишь добавить ноль в конце, но знаете ли вы, что есть фишка как легко умножить двузначное число на 11?
Допустим, нам нужно умножить 63 на 11. Возьмите двузначное число, которое нужно умножить на 11 и представьте между его двумя цифрами место:
6_3
Теперь сложите первую и вторую цифру этого числа и поместите в это место:
6_(6+3)_3
И наш результат умножения готов:
63*11=693
Если же результат сложения первой и второй цифры двузначное число, вставляйте только вторую цифру, а к первой цифре исходного числа прибавляйте единицу:
79*11=
7_(7+9)_9
(7+1)_6_9
79*11=869
2. Быстрое возведение в квадрат числа, оканчивающегося на 5
Если вам нужно возвести в квадрат двузначное число, заканчивающееся на 5, то вы можете сделать это очень просто в уме. Умножьте первую цифру числа на саму себя плюс единица и добавьте в конце 25, и это всё:
45*45=4*(4+1)_25=2025
3. Умножение на 5
Для большинства людей умножение на 5 не составляет труда для небольших чисел, но как быстро считать в уме большие числа, умноженные на 5?
Вам нужно взять это число и разделить на 2. Если результат целое число, то добавьте к нему 0 в конце, если нет, отбросьте остаток и добавьте 5 в конце:
1248*5=(1248/2)_(0 или 5)=624_(0 или 5)=6240 (результат деления на 2 целое число)
4469*5=(4469/2)_(0 или 5)=(2234.5)_(0 или 5)=22345 (результат деления на 2 число с остатком)
4. Умножение на 4
Это очень простая и, с первого взгляда, очевидная фишка умножения любого числа на 4, но несмотря на это люди не догадываются о ней в нужный момент. Чтобы просто умножить любое число на 4, нужно умножить его на 2, а потом снова умножить на 2:
67*4=67*2*2=134*2=268
Лист самоконтроля 6 (5 класс)
1.Как формулируется сочетательный закон умножения?
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
2.Каким равенством выражается сочетательный закон умножения?
(а·b)·c = a·(b·c).
3.Что следует из переместительного и сочетательного законов умножения?
Множители в произведении можно менять местами и заключать в скобки произвольным образом.
4.Что называется: а) кругом; б) центром круга; в) радиусом круга; г) диаметром круга; д) хордой круга?
Круг – это часть плоскости, ограниченная окружностью. Центром круга называется центр этой окружности. Радиусом круга называется радиус этой окружности. Диаметром круга называется диаметр этой окружности. Хордой круга называется хорда этой окружности.
5.Из каких точек состоит: а) окружность; б) круг?
Окружность состоит из точек, удаленных от центра на расстояние, равное ее радиусу.
Круг состоит из точек, удаленных от данной точки (его центра) на расстояние, меньшее или равное его радиусу.
6.Как можно назвать переход от произведения (а +b)·с к сумме а·с +b·с?
Раскрытие скобок.
7. Как можно назвать переход от суммы а·с +b·с к произведению (а +b)·с?
Вынесение общего множителя за скобки
8.Как называются числа 60, 5, 12 в равенстве 60 : 5 = 12?
Делимое, делитель, частное.
9.Что называется частным чисел а и b?
Частным чисел а и b называется такое число p, при умножении на которое числа b получается а: b·p=a.
10.Как называется выражение а : b?
Частное.
11.Чему равно частное а:1?
а:1 = а.
12.Если а – натуральное число, то чему равно частное: а) 0:а; б) а:а?
0:а = 0; а:а= 1
13.Можно ли делить на нуль?
Делить на нуль нельзя!
14.Как найти неизвестный делитель, зная делимое и частное?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
15.Составьте задачу на части по выражению 48:12·(12 + 3 + 8).
На факультативе решались задачи, из которых 12 частей были текстовыми, 3 части – геометрическими и 8 частей – логическими. Сколько всего решено задач на факультативе, если текстовых задач было решено 48?
Лист самоконтроля 7 (5 класс)
1.Что такое квадрат числа а? Куб числа а?
Произведение двух множителей, равных а, называется квадратом числа а.
Произведение трех множителей, равных а, называется кубом числа а.
2.Что такое вторая, третья, пятая степень числа а?
Квадрат числа а – это вторая степень а.
Куб числа а – это третья степень числа а.
Произведение пяти множителей, равных а, называется пятой степенью а.
3. Как читается и что означает выражение аn?
аn– это произведение n множителей, равных а. Читается «а в степени n» или «а в n-й степени».
4.Какую форму имеют грани прямоугольного параллелепипеда?
Прямоугольников.
5.Что называется: а) ребром прямоугольного параллелепипеда; б) вершиной прямоугольного параллелепипеда?
Ребром называется сторона грани, вершиной – вершина грани.
6.Сколько у прямоугольного параллелепипеда: а) граней; б) ребер; в) вершин?
6 граней, 12 ребер и 8 вершин.
7.Что такое измерения прямоугольного параллелепипеда?
Три ребра, которые имеют общую вершину.
8.Как называются измерения прямоугольного параллелепипеда?
Длина, ширина, высота.
9.Что такое куб?
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
10.Как найти неизвестное вычитаемое, зная уменьшаемое и разность?
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
11.Какие действия называют действиями: а) первой ступени; б) второй ступени?
Сложение и вычитание называют действиями первой ступени. Умножение и деление называют действиями второй ступени.
12. Каков порядок выполнения действий при вычислении числовых выражений?
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то эти действия выполняют по порядку слева направо.
2. Если в выражении нет скобок и оно содержит действия разных ступеней, то сначала выполняют умножение и деление (слева направо), а затем сложение и вычитание (слева направо).
3.Если в выражении есть скобки, то сначала выполняют все действия в скобках (слева направо), а затем все действия в полученном выражении (слева направо).
13.Что называется буквенным выражением?
Запись, состоящая из чисел, букв, знаков действий и скобок, называется буквенным выражением.
14.Что такое переменная?
Переменная – это буква, входящая в буквенное выражение, которая может принимать различные значения.
15.Что называется значением выражения с переменными при данных значениях переменных?
Если в выражение с переменными вместо переменных подставить числа, то получится числовое выражение. Его значение называется значением выражения с переменными при данных значениях переменных.
Лист самоконтроля 4
1.Что называется уравнением?
Равенство, содержащее одно неизвестное, называется уравнением с одним неизвестным.
2. Что называют корнем уравнения?
Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называется корнем уравнения.
3.Что значит решить уравнение?
Решить уравнение – это значит найти все его корни.
4.Как найти неизвестное: а) слагаемое; б) уменьшаемое; в) вычитаемое?
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
5. Что называется: а) прямоугольником; б) квадратом?
Четырехугольник, у которого все углы прямые, называется прямоугольником.
Прямоугольник, у которого все стороны равны, называется квадратом.
6.Назовите свойство противоположных сторон прямоугольника?
Противоположные стороны прямоугольника равны.
7. Как называются стороны прямоугольника?
Две стороны прямоугольника, которые имеют общую вершину, называются длиной и шириной. Длина и ширина прямоугольника называются его измерениями.
8.Чему равен периметр Р:а) прямоугольника со сторонами а и b; б) квадрата со стороной а?
Периметр прямоугольника Р= 2·(а +b). Периметр квадрата Р = 4·а.
9.Как установить, равны ли два прямоугольника (квадрата)?
Если при наложении их можно совместить, то они называются равными.
10.Как формулируется распределительный закон умножения относительно сложения?
Произведение суммы чисел и числа равно сумме произведений каждого слагаемого и этого числа.
Чтобы сумму двух чисел умножить на число можно каждое слагаемое умножить на это число и полученные произведения сложить.
11.Каким равенством выражается распределительный закон умножения относительно сложения?
(а +b)·c = a·c + b·c.
12. Как формулируется распределительный закон умножения относительно вычитания?
Чтобы разность двух чисел умножить на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе.
13.Каким равенством выражается распределительный закон умножения относительно вычитания?
(а –b)·c = a·c –b·c.
14.Сформулируйте признак делимости на 2.
Если натуральное число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2. Все остальные натуральные числа на 2 не делятся.
15. Какие числа называются: а) четными; б) нечетными?
Числа, которые делятся на 2 (числа, которые кратны 2), называются четными.
Числа, которые не делятся на 2 (числа, которые не кратны 2), называются нечетными.
Лист самоконтроля 5
1.Как в равенстве 7·4 = 28 называются: а) числа 7 и 4; б) число 28?
Числа 7 и 4 – множители, 28 – произведение.
2.Как называется выражение 7·4?
7·4 – произведение.
3.По какому правилу число а умножают: а) на 1; б) на 0?
а·1 = а, а·0 = 0.
4.Как формулируется переместительный закон умножения?
От перестановки множителей произведение не меняется.
5.Каким равенством выражается переместительный закон умножения?
а·b =b·a.
6.Какой квадрат называется единичным?
Квадрат, сторона которого равна единице измерения длины, называется единичным.
7.Что принимается за единицу измерения площадей?
Площадь единичного квадрата принимается за единицу измерения площадей.
8.Что такое: а) 1 м2, б) 1 см2?
Площадь квадрата со стороной 1 м равна одному квадратному метру.
Площадь квадрата со стороной 1 см равна одному квадратному сантиметру.
9.Чему равна площадь прямоугольника?
Площадь прямоугольника равна произведению его измерений, т. е. произведению длины и ширины. Если измерения прямоугольника а и b, то его площадь S =a·b.
10.Чему равна площадь квадрата?
Если сторона квадрата равна а, то его площадь S =a2.
11.Что такое: а) 1 гектар; б) 1 ар?
1 гектар – это площадь квадрата со стороной 100 м.
1 ар – это площадь квадрата со стороной 10 м.
1 га = 100 а.
12.Что такое: а) радиус окружности; б) хорда окружности; в) диаметр окружности?
Радиус окружности – это отрезок, соединяющий центр окружности с любой точкой на окружности. Хорда окружности – это отрезок, концы которого лежат на окружности. Диаметр окружности – это хорда, проходящая через центр окружности.
13.Как найти неизвестное делимое, зная делитель и частное?
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
14.Что называется: а) числовым выражением; б) значением числового выражения?
Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок. Значением числового выражения называется число, которое получается в результате выполнения всех указанных в этом выражении действий.
15. Что называют признаком?
Признаком называют правило, пользуясь которым удобно выяснить, выполняется ли некоторое свойство.
Лист самоконтроля 6
1. Как формулируется сочетательный закон умножения?
2.Каким равенством выражается сочетательный закон умножения?
3.Что следует из переместительного и сочетательного законов умножения?
4.Что называется: а) кругом; б) центром круга; в) радиусом круга; г) диаметром круга; д) хордой круга?
5.Из каких точек состоит: а) окружность; б) круг?
6.Как можно назвать переход от произведения (а +b)·с к сумме а·с +b·с?
7. Как можно назвать переход от суммы а·с +b·с к произведению (а +b)·с?
8.Как называются числа 60, 5, 12 в равенстве 60 : 5 = 12?
9.Что называется частным чисел а и b?
10.Как называется выражение а : b?
11.Чему равно частное а:1?
12.Если а – натуральное число, то чему равно частное: а) 0:а; б) а:а?
13.Можно ли делить на нуль?
14.Как найти неизвестный делитель, зная делимое и частное?
15.Составьте задачу на части по выражению 48:12·(12 + 3 + 8).
Лист самоконтроля 7
1. Что такое квадрат числа а? Куб числа а?
2.Что такое вторая, третья, пятая степень числа а?
3. Как читается и что означает выражение аn?
4.Какую форму имеют грани прямоугольного параллелепипеда?
5.Что называется: а) ребром прямоугольного параллелепипеда; б) вершиной прямоугольного параллелепипеда?
6.Сколько у прямоугольного параллелепипеда: а) граней; б) ребер; в) вершин?
7.Что такое измерения прямоугольного параллелепипеда?
8.Как называются измерения прямоугольного параллелепипеда?
9.Что такое куб?
10.Как найти неизвестное вычитаемое, зная уменьшаемое и разность?
11.Какие действия называют действиями: а) первой ступени; б) второй ступени?
12. Каков порядок выполнения действий при вычислении числовых выражений?
13.Что называется буквенным выражением?
14.Что такое переменная?
15.Что называется значением выражения с переменными при данных значениях переменных?
Развивающие игры и тренажёры по математике
Упражнение «Мозаик» — тренирует зрительную память
Упражнения «Математик» и «Капли»
Дистанционная олимпиада по математике!
Друзья! Решите предлагаемые ниже задачи и пришлите полученные вами результаты и рассуждения по обратной связи (смотрите в меню сайта «Контакты»). Фамилии участников и набранное ими количество баллов за решение задач будут опубликованы на сайте.
Задания недели :
16. Плоскость окрашена в два цвета. Докажите, что найдутся две точки, отстоящие друг от друга на расстоянии 1 м, окрашенные одинаково.
17. В ящике 100 черных и 100 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было 2 шара белого цвета?
18. Три подруги одеты в белое, зеленое и синее платья. Их туфли также белого, зеленого и синего цветов. Известно, что у Ани цвет платья и туфель совпадали. Ни платье, ни туфли Вали не были белыми. Наташа – в зеленых туфлях. Определите цвет платьев и туфель каждой из подруг.
19. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом находится между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Как распределены эти жидкости по сосудам?
20. Разрежьте фигуру на четыре равные части и сложите из этих частей квадрат с квадратным отверстием посередине:
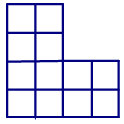
Всем желаем успехов в решении заданий 16-20 нашей олимпиады! Не сдаваться!Ждем ваших сообщений.
www.edu.grsu.by/math Гродненская обл. дист. олимп. по мат. для 5 -7 кл.
IV Дистанционная олимпиада по математике
среди учащихся 5-7 классов
Первый этап прошел с 23 октября по 26 октября 2013 года
5 класс(23-26.10.2013)
1.Двадцать трёхметровых брёвен распилили на полуметровые поленья. Сколько распилов при этом сделали?
Ответ: 100.
2.Расшифруйте ребус
МЯУ + МЯУ = АМУР ,
если разным буквам соответствуют разные цифры, а одинаковым – одинаковые.
В ответ запишите число, которое зашифровано словом
АМУР
Если таких чисел несколько, то в ответ запишите большее число.
Ответ: 1974
3. Сколько всего существует четырехзначных чисел, запись которых начинается цифрой 2?
4. Произведение четного и нечетного чисел является
Ответ 1 нечетным числом
Ответ 2 невозможно определить
Ответ 3 четным числом
Ответ 4 ответ зависит от чисел
5. Сколько квадратов изображено на рисунке?
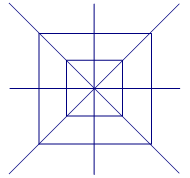
Ответ: 10
6. Запишите наибольшее пятизначное число, у которого цифра в разряде тысяч в 3 раза больше цифры в записи разряда единиц, а цифры в разрядах единиц и сотен одинаковые.
Ответ: 99393
7. Леша задумал однозначное число, умножил его на 17, а результат умножил на 2017 и получил число, последняя цифра которого равна 3. Какое число задумал Леша?
Ответ: 7
8. Из какого четырехзначного числа надо вычесть 2013, чтобы получить наибольшее трехзначное число?
Ответ: 3012
9. Если округлить число 2 013 689 до десятков, то получим число
Ответ 1 2 013 680
Ответ 2 2 013 699
Ответ 3 2 013 700
Ответ 4 2 013 690
Ответ 5 2 013 600
10. Чему равна сумма 1 + 2 + 3 + …+ 2013?
Ответ: 2027091
11. Малыш сказал Карлсону, что угостит его вареньем, только если тот справится с предложенной им задачей. Малыш загадывает три цифры, а Карлсон говорит ему три числа, каждое из которых не больше 150. Малыш поочередно умножает свои цифры на числа Карлсона, складывает получившиеся произведения и результат говорит Карлсону. Если Карлсон отгадывает каждое из задуманных Малышом цифр, то получает банку варенья. Назовите сумму чисел, которые должен назвать Карлсон, чтобы получить угощение вне зависимости от того, какие цифры задумает Малыш.
Ответ: 111
12. Периметр треугольника равен 2013 см. Найдите длину меньшей стороны (в см) этого треугольника, если одна из его сторон больше другой на 17 см и меньше третьей на 29 см.
В ответ запишите только число.
Ответ: 650
Контрольная работа № 2
к главе 2 «Сложение и вычитание натуральных чисел»
Вариант 1
1.Укажите неверные равенства.
а) а – 0 = 0 – а б) а – (b– с) = а– b+ с
в) а + (b+ с) = а+ b+ с г) а + 0 = 0 + а
Ответ: а).
2.Запишите названия не менее трех треугольников, изображенных на рисунке 83.
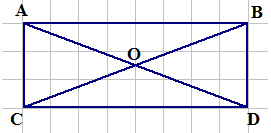
Рис. 83
Ответ:треугольникиАОС, АОВ, АВС.
3.По рисунку 84 запишите названия не менее трех:
1) развернутых углов;
2) прямых углов;
3) смежных углов;
4) вертикальных углов.
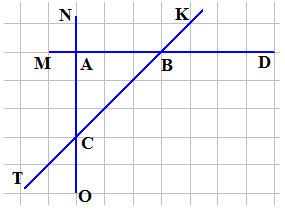
Рис. 84
Ответ:1) углы ТСК, КВТ, MAD;
2) углы МАО, MAN, NAD.
3) углы ТСО и ОСК, KBD и DBT, KBD и KBM.
4) углы KBD и MBT, TCO и NCK, NAB и MAO.
4. Найдите значение выражения:
1) 155 871 + 48 124; 2) 16 247 – 9584;
3) 90 845 712 – 31 837 605; 4) 6 398 451 + 3 502 049.
Ответ: 1) 155 871 + 48 124 = 203 995; 2) 16 247 – 9584 = 6663;
3) 90 845 712 – 31 837 605 = 59 008 107; 4) 6 398 451 + 3 502 049 =9 900 500.
5. Выполните действия:
1) 4279 + 104 + 1721;
2) 638 + 84 757 + 362 + 115 243;
3) (16 247 + 7575 + 3753) – (2442 + 2775 + 12 358).
Ответ: 1) 4279 + 104 + 1721= 6404;
2) 638 + 84 757 + 362 + 115 243 = 201 000;
3) (16 247 + 7575 + 3753) – (2442 + 2775 + 12 358) = 10 000.
6. Решите уравнение:
1) а – 564 = 87; 2) 1000 – b= 791;
3) х + 419 = 839; 4) 7100 = 3500 + t.
Ответ: 1) 651; 2) 209; 3) 420; 4) 3600.
7. Решите уравнение:
1) 843 + (950 + m) = 3793; 2) (2505 – p) – 750 = 1005.
Ответ:1) 2000; 2) 750.
8.Решите задачу с помощью уравнения.
К задуманному числу прибавили 180, затем вычли 60 и получили 140. Какое число задумали?
Ответ:20.
9.*В январе завод «Горизонт» выпустил на 148 телевизоров меньше, чем в феврале, а в марте – на 204 телевизоров больше, чем в феврале. Сколько телевизоров выпускали каждый месяц, если всего за три месяца завод выпустил 3500 телевизоров?
Ответ:1000; 1148; 1352.
10.* Найдите сумму двух чисел, если она больше одного из них на 15 и больше другого из них на 35.
Ответ:50.
С.2.3. Сочетательный закон сложения
5.*Найдите сумму (разными способами):
10 + 50 + 90 + … + 210 + 250 + 290.
Решение.
10 + 50 + 90 + … + 210 + 250 + 290 =
=10 + 50 + 90 + 130 + 170 + 210 + 250 + 290 =
=(10 + 290) + (50 + 250) + (90 + 210) +(130 + 170) =
=300 + 300 + 300 + 300 = 300·4 = 1200.
Ответ: 1200.
С.2.9. Задачи на нахождение двух чисел по их сумме и разности
5.*Поставьте между цифрами в левой части равенства
5555555 =620
Знаки «+» так, чтобы равенство было верным.
Ответ: 555 + 55 + 5 + 5 = 620.
С.2.10. Уравнение
5.*Ира спросила Таню: «Сколько этажей в твоем доме?» Таня ответила: «Я живу на пятом этаже, но если считать с верхнего этажа, то на восьмом». Сколько этажей в доме Тани?
Решение.
При таком подсчете пятый и восьмой этажи совпадают. Значит, над пятым этажом Таниного дома 8 – 1= 7 этажей. Следовательно, в доме 5 + 7 = 12 этажей.
Ответ: 12 этажей.
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка в инстаграм