Дистант
Третья олимпиада по математике «Гимназист – 2015»
В конце каждого учебного года в гимназии № 1 г. Ивье проводится открытая математическая олимпиада для учащихся 4 – 10 классов, в которой могут участвовать все желающие школьники, лицеисты и гимназисты Ивьевского района. Олимпиада предоставляет возможность учащимся соотнести свои знания со знаниями сверстников, развить свои способности, почувствовать атмосферу конкурса, получить дипломы и сертификаты участников по электронной почте, а также интересно и с пользой провести время. Школьники – победители и призеры из каждой параллели – станут кандидатами на зачисление в гимназию № 1 г. Ивье, где имеются прекрасные условия для занятий математикой: в образовательном процессе применяются современные информационные технологии http://moodle.edu.by Национального института образования Министерства образования Республики Беларусь, предоставляются возможности углублять и расширять свои знания по математике в классах физико-математического направления, в факультативах «Готовимся к олимпиадам по математике», принимать участие в научно-исследовательской работе, в Международной математической олимпиаде "Формула Единства – Третье тысячелетие", второй очный тур которой в Гродненской области проходит в гимназии № 1 г. Ивье. Ивьевские гимназисты успешно участвуют в дистанционных олимпиадах школы точных наук и в олимпиадах абитуриентов по математике Гродненского государственного университета имени Янки Купалы – на различных этапах 32 человека показали лучшие результаты в области. В интернет-олимпиадах по математике Санкт-Петербургской академии постдипломного педагогического образования в текущем учебном году они награждены 24 дипломами победителей и призеров. В Московской областной общеобразовательной школе естественно-математической направленности имени П. Л. Капицы гимназисты из г. Ивье в 2015 году удостоены 7 дипломов II и III степени, в олимпиаде по математике Санкт-Петербургского национального исследовательского университета ИТМО трое гимназистов в этом году прошли на очный тур. В Международной интернет-олимпиаде «Сократ» победителями и призерами стали 54 ивьевских гимназиста. Трое учащихся-одиннадцатиклассников получили поощрительный отзыв на республиканской научно-практической конференции за научно-исследовательскую работу «Семь разных доказательств теоремы Птолемея, ее обобщения и применения». Команда гимназии стала призером математической интернет-карусели.
Сегодня гимназия № 1 г. Ивье объявляет о начале своей третьей олимпиады по математике для учащихся 4 – 10 классов. Председатель оргкомитета – Кот Вацлав Иванович, кандидат педагогических наук, учитель математики квалификационной категории «учитель-методист», отличник образования Республики Беларусь. Олимпиада «Гимназист – 2015» пройдет в два тура (первый – заочный, второй – очный).
Условия задач первого тура олимпиады по математике
4 класс
1.В супермаркете проходит рекламная акция: покупая 2 шоколадки, третью шоколадку покупатель получает в подарок. Шоколадка стоит 7 тысяч рублей. Какое наибольшее количество шоколадок может получить покупатель, имея 65 тысяч рублей?
2. Во дворе 20 утят и поросят, у них вместе всего 48 ног. Во сколько раз утят больше, чем поросят?
3. Двум братьям вместе 40 лет. Сколько лет старшему брату, если половина лет одного равна трети лет другого? Дайте ответ в годах.
4. В коробке 19 шаров – белых, красных и чёрных. Белых в 8 раз больше, чем красных, а чёрных меньше, чем красных. Сколько в коробке красных шаров?
5. Сколько двузначных чисел, делящихся на 3, у которых цифра десятков на 2 меньше цифры единиц?
6. Расшифруйте ребус: AC + CB = ABC. Одинаковые буквы – это одинаковые цифры, разные буквы – разные цифры. Назовите значение суммы: A + B + C.
5-6 классы
1. На рынке два апельсина можно поменять на три банана. Два банана можно поменять на четыре груши. А на сколько апельсинов можно поменять три груши?
2. Код замка кейса записывается четырёхзначным числом с четырьмя различными цифрами. Если у него зачеркнуть первую и последнюю цифры, то получится наименьшее двузначное число из тех, у которых сумма цифр равна 12. А если зачеркнуть две средних, то получится двузначное число, у которого последняя цифра в 3 раза больше первой. Напишите код для открывания кейса.
3. В магазине продаются шоколадки в виде букв. Одинаковые буквы стоят одинаково, а разные – по-разному. Известно, что слово ЛЕВ стоит 6 рублей, слово СОВА стоит 10 рублей, а слово БЕЛКА стоит 11 рублей. Сколько стоит слово СОБАКА?
4. Миша нашёл большой газетный лист. Сначала он разорвал этот лист на 5 частей. Затем некоторые из получившихся кусочков порвал на 3 или 5 частей каждый. Затем ещё несколько кусочков порвал на 3 или 5 частей каждый. И повторил это действие несколько раз. Сколько могло в итоге получиться кусочков? Укажите все подходящие варианты ответов: 48; 49; 50; 51; 52; ни один из перечисленных.
5. Чародей завел себе животных трёх видов. Все животные, кроме двух, – Единороги; все, кроме двух, – Фениксы; остальные – Драконы. Сколько питомцев живёт у Чародея?
6. У Весёлой бабки Ёжки в синей избушке живут 5 гусей, а у Задорной бабки Ёжки в красной избушке живут 10 гусей. Их избушки соединяет прямая дорога длиной 300 метров. Чтобы не тратиться, бабки Ёжки решили построить для всех гусей общую большую кормушку у дороги. Причём таким образом, чтобы сумма расстояний, которые все гуси будут пробегать во время кормёжки от своей избушки до кормушки, была наименьшей. На каком расстоянии от синей избушки Ёжкам нужно поставить кормушку?
7-8 классы
1.Сумма двух чисел 715. Одно число заканчивается нулём. Если этот нуль зачеркнуть, то получится второе число. Найдите большее число.
2. На доске написан ребус ВВВ – ББ + А = 620. Каждая буква заменяет одну цифру. Чему же равна сумма А+ Б + В?
3. Сегодня на кольцевом маршруте в одном направлении работало 6 автобусов с интервалом движения 12 минут. Какой интервал движения автобусов будет завтра, если к ним добавится ещё 2 таких же автобуса?
4. Робинзон попал на необитаемый остров. Каждый день (начиная со второго дня пребывания на острове) он вырезал на доске первую букву названия дня недели на русском языке. На 2014–й день, вырезав букву, он посчитал вырезанные буквы. Оказалось, что разных букв было вырезано разное количество. В ответ запишите день недели, когда Робинзон попал на остров.
5. Биссектриса угла при основании равнобедренного треугольника равна основанию. Чему равны углы этого треугольника?
6.Миша сам с собой играет в такую игру. За ход разрешается брать из кучи спичек ровно 5, 11 или 13 спичек, до тех пор, пока это возможно. Сначала в кучке лежало 108 спичек, а в конце игры не осталось ни одной. За какое минимальное количество ходов могла закончиться игра?
9-10 классы
1.Сергей написал на доске такое выражение: 2*1*4*3*6*5*8*7*10*9. Полина стерла все звездочки и вместо каждой звездочки написала какой-нибудь знак: "+" или "-". Затем ребята вычислили значение выражения, написанного на доске. Какие числа у них могли получиться: 11, 12, 23, 45, 48, 51, 53, 59?
2. Однажды на острове рыцарей и лжецов все 47 островитян собрались вокруг большого костра. Уселись они кружком и стали бурно обсуждать, стоит ли звать спящего приплывшего к ним в гости Кука. Да так расшумелись, что каждый слышал только себя, своего соседа слева и соседа справа, а слова остальных не мог расслышать. Из-за шума Кук проснулся и пришёл к ним сам. Посмотрел на это собрание и спросил: "И вы все рыцари?" Его вопрос все островитяне услышали и хором ответили: "Все, кого я не слышу, – лжецы". Сколько же рыцарей было?
3. Если в геометрической прогрессии b3 = 2, то чему равно произведение b1b2b3b4b5?
4. Биссектриса угла B параллелограмма ABCD пересекает сторону AD в точке K так, что AK = 6, DK = 8. Найдите площадь параллелограмма, если величина угла B равна 150°.
5. Процедура «парсум» заменяет тройку чисел тройкой их попарных сумм. Например, тройку чисел {3, 4, 6} она заменяет на тройку {10, 9, 7}, а затем эту тройку – на тройку {16, 17, 19} и т. д. Если начать применять процедуру «парсум» к тройке чисел {20, 1, 5}, то какова будет наибольшая разность между двумя из трёх чисел, полученных после 2015 применений этой процедуры?
6. Из города B выехал велосипедист, через 10 ч из города A навстречу ему выехал второй велосипедист. При встрече оказалось, что первый велосипедист проехал на 45 км больше второго. Продолжая путь с той же скоростью и без остановок, второй велосипедист прибыл в B через 7 ч после встречи, а первый велосипедист в A – через 8 ч после встречи. Определите скорость (в км/ч) второго велосипедиста.
Все участники первого заочного тура олимпиады «Гимназист – 2015» отправляют свои решения до 22 апреля с. г. включительно на электронный адрес [email protected] в виде одного файла формата Microsoft Word. В начале файла с решением следует указать ФИО, школу и класс учащегося, ФИО учителя. Пример названия файла: Иванов_Иван_Иванович_10_класс_Юратишки.doc. Файл следует присылать в виде вложения к электронному письму в формате .doc, .docx. Отсканированное (сфотографированное) решение – в формате .jpg или .pdf
На заключительный второй очный тур олимпиады «Гимназист – 2015», который пройдет в День открытых дверей в гимназии № 1 г. Ивье 25 апреля 2015 года в 10.00 часов, приглашаются все участники первого заочного тура, призеры II этапа республиканской математической олимпиады и районной конференции учащихся по математике 2014/2015 учебного года. Желаем всем успехов!
Дистанционная олимпиада по математике!
Задания недели и их решения:
21.Игра с шоколадкой
Двое по очереди ломают шоколадку 6*8. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре: первый или второй?
Решение:
При правильной игре выигрывает первый. Опишем его стратегию. Первому надо первым ходом разделить шоколадку на две равные части, это он может сделать двумя способами. Затем какой бы ход ни сделал второй, первый может сделать "симметричный" ход, т.е. найти часть, равную той, которую делил второй и разделить её так же, как делил второй.
Ответ: первый.
22. Игра с тремя кучками камней
Имеется три кучки камней: в первой - 10, во второй - 15, в третьей - 20. За ход разрешается разбить любую кучку на две меньшие; проигрывает тот, кто не сможет сделать ход. Кто выигрывает при правильной игре: первый или второй?
Подсказка:
После каждого хода число кучек увеличивается на 1.
Решение:
После каждого хода число кучек увеличивается на 1, следовательно, в конце будет 10 + 15 + 20 = 45 кучек, т.е. будет сделано 42 хода, причем последний ход будет у второго. Итак, выигрывает второй. Интересно отметить, что его выигрыш не зависит от стратегии игроков.
Ответ:второй.
23. Игра с двумя кучками конфет
В двух кучках лежат по 100 конфет. За ход можно взять любое количество конфет из одной кучки. Выигрывает взявший последнюю. Кто выигрывает при правильной игре: первый или второй?
Решение:
Какой бы ход ни сделал первый, у второго есть возможность взять то же число конфет из другой кучки, следовательно, последний ход будет у второго.
Ответ: второй.
24. Из стакана с молоком в стакан с чаем перелили ложку молока. После этого из стакана с чаем перелили обратно в стакан с молоком такую же ложку полученной смеси. Чего теперь больше: молока в стакане с чаем или чая в стакане с молоком? (Количество жидкости в стаканах могло быть разным, перемешивать могли не очень тщательно.)
Указание. Заметьте, что после переливаний количество жидкости в каждом стакане осталось таким же, каким оно было до переливаний.
Решение. Посмотрим на стакан с молоком. В нем жидкости столько же, сколько было изначально, но часть молока заменилась чаем. А куда же делось это молоко? Перешло в стакан с чаем! То есть сколько чая пришло в стакан с молоком, столько и молока этот чай вытеснил в стакан с чаем.
Ответ. Чая в стакане с молоком столько же, сколько молока в стакане с чаем.
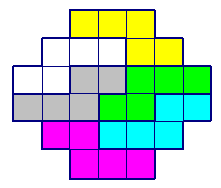
25. Разделите фигуру на шесть равных частей:
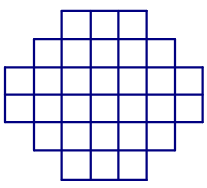
Решение.
Задания недели и их решения:
16.Плоскость окрашена в два цвета. Докажите, что найдутся две точки, отстоящие друг от друга на расстоянии 1 м, окрашенные одинаково.
Решение.Рассмотрите равносторонний треугольник (сделайте рисунок) со стороной 1 м. Из трех его вершин две окрашены одинаково, расстояние между ними как раз и равно 1 м.
17.В ящике 100 черных и 100 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было 2 шара белого цвета?
Решение.
Может случиться так, что вначале мы вытянем 100 черных шаров, и лишь затем 2 белых.
Ответ:102 шара.
18. Три подруги одеты в белое, зеленое и синее платья. Их туфли также белого, зеленого и синего цветов. Известно, что у Ани цвет платья и туфель совпадали. Ни платье, ни туфли Вали не были белыми. Наташа – в зеленых туфлях. Определите цвет платьев и туфель каждой из подруг.
Решение.
Будем решать задачу, последовательно заполняя таблицу:
| Имена девочек | Цвет туфель | Цвет платья | ||||
| белый | зеленый | синий | белый | зеленый | синий | |
| Аня Валя Наташа | Да (3) Нет(2) | Да (1) | Да (4) | Да (5) | Да (6) | Да (7) |
1) Так как у Наташи туфли были зеленого цвета (1), а у Вали не белого (2), то у Ани туфли белые (3), а у Вали синие (4).
2) Так как у Ани цвета платья и туфель совпадали, то у нее платье белое (5), а у Вали платье не синее (так как у нее цвета платья и туфель не совпадают) и не белое (как у Ани), следовательно, оно зеленое (6). У Наташи – платье синее (7).
Ответ:у Ани туфли и платье белые; у Вали туфли синие, а платье зеленое; у Наташи туфли зеленые, а платье синее.
19.В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом находится между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Как распределены эти жидкости по сосудам?
Решение.
Имеются следующие сведения:
1) вода и молоко не в бутылке;
2) сосуд с лимонадом находится между кувшином и сосудом с квасом, следовательно, лимонад не в кувшине и квас не в кувшине;
3) в банке – не лимонад и не вода;
4) стакан находится около банки и сосуда с молоком, следовательно, молоконе в стакане и не в банке.
Результаты запишем в таблицу:
| Бутылка | Стакан | Кувшин | Банка | |
| Молоко | Нет (из 1) | Нет (из 4) | Да (из 5) | Нет (из 4) |
| Лимонад | Да (из 6) | Нет (из 6) | Нет (из 2) | Нет (из 3) |
| Квас | Нет (из 6) | Нет (из 2) | Да (из 6) | |
| Вода | Нет (из 1) | Да (из 6) | Нет (из 5) | Нет (из 3) |
5) из таблицы видно, что молоко может быть только в кувшине, и, следовательно, в кувшине не вода. Продолжим заполнение таблицы;
6) вода не в кувшине, значит, вода может быть только в стакане, следовательно, в стакане не лимонад и не квас, поэтому лимонад в бутылке, а квас в банке.
Ответ:молоко в кувшине, лимонад в бутылке, квас в банке, вода в стакане.
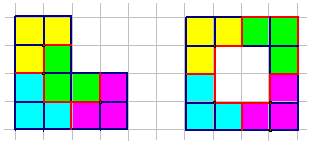
20.Разрежьте фигуру на четыре равные части и сложите из этих частей квадрат с квадратным отверстием посередине:
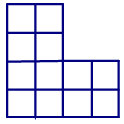
Ответ:
Задания недели и их решения:
11.Расстояние между двумя городами 320 км. Из этих городов одновременно выходят навстречу друг другу два поезда, причем скорость одного из них 45 км/ч, а другого – 35 км/ч. Одновременно с первым поездом вылетел почтовый голубь и со скоростью 50 км/ч полетел навстречу второму поезду, встретив его, он повернул назад и полетел навстречу первому и т. д. Какое расстояние пролетит голубь до момента встречи поездов?
Решение.
Каждый час поезда сближаются на 80 км. Встретились они через 4 ч. За это время голубь пролетел 200 км.
Ответ: 200 км.
12.О каждом из островитян А, В и С известно, что он либо Рыцарь (который всегда говорит правду), либо Лжец (который всегда лжет). Островитянин А говорит: «Мы все Лжецы». Островитянин В говорит: «Ровно один из нас Лжец». Можно ли определить, кто островитянин В – Рыцарь или Лжец? Можно ли определить, кто островитянин С – Рыцарь или Лжец?
Решение.
1) А говорит: «Мы все Лжецы». Если это правда, то, значит, и А – Лжец,а Лжецы не говорят правду. Таким образом, фраза «Мы все лжецы» не может быть правдой. Поэтому точно А – Лжец. Значит, его фраза «Мы все Лжецы» означает, что из А, В и С не все Лжецы, т. е. кто-то Рыцарь.
2) Следовательно, либо А – Рыцарь, либо С – Рыцарь (либо они оба Рыцари).
3) Если В – Рыцарь (т. е. его фраза «Ровно один из нас Лжец» правда), то Лжец один А, а С – также Рыцарь.
4) Если В – Лжец, то Лжецов двое (так как все трое не могут одновременно быть ни лжецами, ни рыцарями), следовательно, С может быть только Рыцарем, независимо от того, кто В(Лжец или Рыцарь).
5) Про В невозможно точно сказать, Рыцарь он или Лжец.
Ответ:кто островитянин В – Рыцарь или Лжец – определить невозможно, островитянин С – Рыцарь.
13.Как набрать из озера восемь литров воды, имея девятилитровое и пятилитровое ведра?
Решение.
Ход решения представим в виде таблицы:
Ведро | 0 шаг | 1 шаг | 2 шаг | 3 шаг | 4 шаг | 5 шаг | 6 шаг |
5 л | 0 | 0 | 5 | 0 | 4 | 4 | 5 |
9 л | 0 | 9 | 4 | 4 | 0 | 9 | 8 |
Переливания можно записать и в виде пар чисел:
(0;0), (0;9), (5;4), (0;4), (4;0), (4;9), (5;8), где первое число в каждой паре – содержимое 5-литрового ведра, второе – 9-литрового.
Ответ: переливания:(0;0), (0;9), (5;4), (0;4), (4;0), (4;9), (5;8), где первое число в каждой паре – содержимое 5-литрового ведра, второе – 9-литрового.
14.В сенате заседают 100 сенаторов. Каждый из них либо продажен, либо честен. Известно, что:
1) по крайней мере один из сенаторов является честным;
2) из каждой произвольно выбранной пары сенаторов по крайней мере – один продажен.
Можно ли с помощью этих двух утверждений определить, сколько сенаторов в этом сенате честных, а сколько – продажных?
Решение.
Из факта 1) следует, что из 100 сенаторов есть 1, который честный.
Рассмотрим 99 пар сенаторов, в каждой из которых присутствует честный сенатор и один из других сенаторов (в каждой паре другой, не встречавшийся ранее). Так как в соответствии с фактом 2) в каждой произвольно выбранной паре сенаторов хотя бы один продажен, то в этих 99 парах все сенаторы, кроме одного честного, продажны. Следовательно, в сенате 99 продажных сенаторов и ровно 1 честный сенатор.
Ответ: да, среди 100 сенаторов 99 продажных и 1 честный.
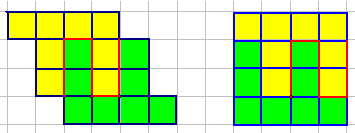
15.Разделите фигуру на две равные части так, чтобы из них можно было составить квадрат:
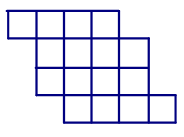
Ответ:
Задания недели и их решения:
6.Из трех старых оловянных ложек и ножа получится 10 оловянных солдатиков; из ложки, двух вилок и двух ножей – 9; из двух вилок и ножа – 5 солдатиков. Сколько оловянных солдатиков получится из двух ложек, двух вилок и двух ножей?
Решение.
Ложку обозначим л, нож – н, вилку – в, солдатик – с. Тогда
3л+1н=10с
1л+2в+2н=9с
2в+1н=5с
Если сложить отдельно левые части равенств и отдельно правые части равенств, то получим 4л + 4н +4в = 24с. Отсюда 2л+2в+2н = 12с.
Можно рассуждать и по другому:
1)10с+5с=15с из 3л+2в+2н
2)15с-9с=6с из 3л+2в+2н-1л-2в-2н=2л
3)6с:2=3с из 2л:2 =1л.
4) 9с+3с=12с из 1л+2в+2н+1л=2л+2в+2н.
Ответ:12 солдатиков.
7. Имеется 11 яблок. С помощью весов можно определить массу любых двух яблок. Как с помощью семи взвешиваний определить общую массу всех яблок?
Решение.
1) Взвесим 8 яблок по 2 штуки и запишем вес каждой пары. Это 4 взвешивания
2) Из оставшихся трех яблок одно пометим, а затем взвесим каждое непомеченное (из 2 оставшихся) с помеченным. Запишем результаты взвешиваний этих пар. Здесь мы выполнили еще 2 взвешивания.
3) Потом взвесим два непомеченных яблока и запишем результат взвешивания. Это уже седьмое взвешивание.
4) Сложим три пары яблок: вес двух непомеченных яблок, вес одного помеченного с непомеченным и вес другого помеченного с непомеченным. В результате в общей сумме масса каждого из трех будет присутствовать дважды, Затем разделим эту массу пополам и получится масса трех яблок(помеченного и двух непомеченных), которую сложив с массой 8 яблок получим окончательный ответ.
8. Какая цифра стоит в числе 345 673 456 734 567… на 100-м месте? На 2015-м месте?
Решение.
В данном случае повторяется одна и та же группа цифр 34567 . С 1-го места по 15-е место в данном числе и с 16-го по 30-е место, с 31-го места по 45-ое и т. д. повторяются все эти 15 цифр. Значит, на 10-м, на 25-м, на 40-м, на 55-м, на 70-м, на 85-м и на 100-м месте стоит цифра 7.
2015:15 =134(ост.5). Значит, на 5-м месте стоит цифра 7, на 20-м, на 35 и т. д., на 5+134·15 = 2015 стоит цифра 7.
Ответ:7.
9.У Антона и Саши – 17 наклеек, у Саши и Никиты – 18 наклеек, а у Антона и Никиты – 25 наклеек. Сколько наклеек у каждого мальчика?
Решение.
Обозначим количество наклеек у Антона А, у Саши С, у Никиты Н.
А+С=17
С+Н=18
А+Н=25
2А+2С+2Н=17+18+25, т. е. 2(А+С+Н)=60 – удвоенное количество наклеек у мальчиков. Значит, А+С+Н =60:2 =30(наклеек) у Антона, Саши и Никиты.
30 – 17 = 13(наклеек) у Никиты,
30 – 18 = 12 (наклеек) у Антона,
30 – 25 = 5 (наклеек) у Саши.
Ответ:у Антона 12 наклеек, у Саши 5 наклеек, у Никиты 13 наклеек.
10. Андрей задумал число. Он прибавил к нему 5, затем полученное число разделил на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Андрей?
Решение.
Решим задачу с конца, выполняя действия, обратные тем, что делал Андрей: (2·7+6):4·3 – 5= 20:4·3 – 5=15 – 5=10. Значит, Андрей задумал число 10.
Ответ:10.
Задания недели и их решения:
1.Для нумерации страниц в учебнике потребовалось 787 цифр. Какой номер имеет последняя пронумерованная страница, если первая пронумерованная страница имеет номер 3?
Решение.
Однозначных чисел (3, 4, 5, 6, 7, 8, 9) всего 7.
Двузначных чисел (10, 11, 12, …, 99) всего 90.
На нумерацию страниц однозначными и двузначными числами использовано 7 + 90·2 = 187 цифр.
Значит, на нумерацию трехзначными числами пошло 787 – 187 = 600 цифр, а чисел – 600: 3 = 200. Отсчитаем 200 трехзначных чисел: первое такое число 100, прибавим к нему еще 199 и получим последнее трехзначное число 299. Следовательно, последняя пронумерованная страница имеет номер 299.
Ответ: номер 299.
2. На лугу ребята пасут жеребят. Если пересчитать ноги ребят и жеребят, то получится 184, а если считать головы, то 53. Сколько на лугу ребят и сколько жеребят?
Решение.
Пусть все жеребята встанут на задние ноги, тогда все (ребята и жеребята) будут стоять на двух ногах и их будет 53·2 = 106. Тогда 184 – 106 = 78 – количество поднятых ног жеребятами и 78:2 = 39 – количество жеребят на лугу. Следовательно, 53 – 39 = 14(ребят).
Ответ: 14 ребят, 39 жеребят.
3. Гусеница ползла вверх по дереву. За день она успевала проползти 3 м, а за ночь опускалась на 2 м. На какой день она достигла высоты 7 м?
Решение.
За сутки (за день и ночь) гусеница поднималась на 3 – 2 = 1(м).
За 4 суток она поднимется на 1·4 = 4 (м).
На 5-й день она поднимется на 4 + 3 = 7 (м).
Ответ: на 5-й день.
4. Из 10 листиков бумаги некоторые разрезали на 4 части. Получили всего 31 листик. Сколько листиков бумаги разрезали?
Решение.
Если разрезать 1 листик на 4 части (останется 9 целых листиков), то получим 4 + 9 = 13 листиков.
Если любые из 2 имеющихся листиков разрезать на 4 части, то получится 4·2 + 8 = 16 листиков.
Если любые из 3 имеющихся листиков разрезать на 4 части, то получится
4·3 + 7 = 19 листиков.
31 листик получится, если любые из 7 имеющихся листиков разрезать на 4 части каждый (4·7 + 3 = 31).
Ответ: 7 листиков.
5. Собака преследует зайца, который находится впереди нее на 40 своих прыжков. Собака делает 7 прыжков за то время, за которое заяц делает 9 прыжков, но 3 прыжка собаки равны 5 прыжкам зайца. Сколько прыжков надо сделать собаке, чтобы догнать зайца?
Решение. По условию 3 прыжка собаки равны 5 прыжкам зайца, следовательно, 21 прыжок собаки равен 35 прыжкам зайца. Заметим, что собака делает 7 прыжков за то время, за которое заяц делает 9 прыжков, значит, собака делает 21 прыжок за то время, за которое заяц делает 27 прыжков. Известно, что 21 прыжок собаки равен 35 прыжкам зайца, следовательно, собака, сделав 21 прыжок, приближается к зайцу на 8 заячьих прыжков. Сделав 105 прыжков, собака приблизится к зайцу на 40 заячьих прыжков, т. е. догонит зайца.
Другая запись решения
1 прыжок собаки обозначим 1с, 1 прыжок зайца – 1з.
7с – 9з, а 3с = 5з.
НОК(3;7) = 21
21с – 27з, а 21с = 35з
35з – 27з = 8з – на столько приблизилась собака.
8з·5 = 40з, когда 21с·5 = 105с.
Ответ: 105 прыжков собаки.
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка подписчиков инстаграм