№ 17 профиль ЕГЭ
 Локация
Главная страница Карта сайта
Локация
Главная страница Карта сайта
Прототипы задания 17 профиля ЕГЭ -2021
Тема заданий № 17 "Финансовая математика"
Типы заданий № 17: Задачи на оптимальный выбор Банки, вклады, кредиты
За это задание ты можешь получить 3 балла. Пояснения здесь На решение дается около 35 минут. Уровень сложности: повышенный. Средний процент выполнения: в 2019 году 15.4%, в 2020 году 22,0%. Ответом к заданию 17 по математике должен быть развернутый ответ (полная запись решения с обоснованием выполненных действий). Требования ФИПИ к профильному уровню здесь
Что требуется в № 17? Решить текстовую задачу преимущественно экономического содержания на кредиты, вклады и оптимальный выбор. Особенности задания. Задача 17 это текстовая задача, в которой ученикам предстоит работать с экономическими моделями. Основные сложности данного задания: запутанное условие, в некоторых случаях требующее дополнительных теоретических знаний о процессе начисления банковских процентов, работе со множествами; уравнение с большими и неудобными числами (в некоторых задачах будут фигурировать миллионы). Все это является особенностью любой текстовой задачи, поэтому важно в первую очередь уметь упорядочивать и визуализировать данные. Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль. Полезные советы. Внимательно читайте условие задачи, вникайте в процедуры выдачи кредита или открытия вклада, которые там описываются. Каждый пункт условия сразу переводите в уравнение. Таким образом вы получите уравнение или систему уравнений, которые вам останется только решить. Чтобы подготовиться, изучите основные схемы кредитования с дифференцированными и аннуитетными платежами. В задачах оптимизации нужно уметь работать с линейными/нелинейными целевыми функциями с целочисленными/нецелочисленными точками экстремумов.
Критерии оценивания № 17:
| Балл | Критерии |
| 3 | обоснованно получен верный ответ |
| 2 | верно составлена математическая модель,но допущена вычислительная ошибка при решении |
| 1 | не до конца составлена математическая модель, а также если найдете ответ подбором |
| 0 | решение не соответствует ни одному из критериев, представленных выше. |
Задача 17 появилась в ЕГЭ в 2015 году. Тогда в сфере ЕГЭ по математике произошли сразу две вещи: был введён базовый экзамен и усложнён профильный. В качестве главного усложнения как раз выступила 17 задача. Ни в одном стандартном учебнике, по которым учатся современные школьники, не разбирается подобных задач. Это уникум, порождённый ЕГЭ. В итоге отличник, который честно начал готовиться к экзамену заранее, обнаруживает для себя в 10-11 классах целый пласт новых сложных задач, который ему нужно освоить параллельно с программой старших классов, потому что решается эта задача методами 8-го.
Решение № 17 включает здесь здесь здесь здесь здесь здесь здесь
x*(1 + p/100) - величина x увеличилась на p%
x*(1 - k/100) - величина x уменьшилась на k%
x*(1 + p/100)k - величина x увеличилась на p% k раз
x*(1 + p/100)*(1 - k/100) – величина х сначала увеличилась на p%, а потом уменьшилась на k%
Задачи на погашение кредита равными платежами:
Размер кредита принимаем за х, процент банка а, выплата по кредиту S.
Через год после начисления процентов и выплаты суммы S размер долга x * (1 + a/100) -S.
Размер долга через 2 года: (xp – S)p – S, где p = 1 + a/100
Размер долга через 3 года: ((xp – S)p – S)p – S
Размер долга через n лет: xpn – S(pn-1+ … + p3 + p2 + p + 1)
Определение процента здесь и примеры здесь и здесь Нахождение процента от числа здесь и примеры здесь Нахождение дроби от числа здесь и примеры здесь Процентное изменение величины здесь и примеры здесь Простые проценты здесь и примеры здесь Сложные проценты здесь и здесь и примеры здесь и здесь и здесь и здесь
Заметим, что на реальном ЕГЭ могут попадаться и знакомые вам задачи. Уже известная всем задача чаще всего попадается под № 13 и № 17. В остальных номерах второй части ЕГЭ вероятность встретить что-то новенькое (не обязательно сложное новое) выше. Разберем те задачи под № 17, которые попадались на настоящих ЕГЭ несколько раз. ТОП-4 самых популярных задач № 17:
1) Про дифференцированные платежи: условие здесь решение здесь + здесь (О.С.В.-общая сумма выплат).
2) Про разные платежи: условие здесь решение здесь
3) Про равные платежи условие здесь решение здесь
4) Из книг Ященко про фермера (оптимизация) условие здесь решение здесь
Сканы решений № 17 участниками ЕГЭ 2020: 1) поставили 3 из 3 баллов здесь 2) 2 из 3 баллов здесь 3) 1 балл из 3 здесь и здесь 4) 0 баллов из 3 здесь
Как лишиться баллов за решение задачи 17? Если задача нешаблонная, то просто сразу пропускайте. Если шаблонная, то можно перепутать кредитную схему; ошибиться в расчетах и единицах измерения, если не по ходу задачи, то хотя бы в конечном ответе; сделать логическую ошибку, например условие «выплата за каждый из трех периодов меньше 3000» записать как « суммарные выплаты за все три периода меньше 9000». И вуаля: 0 баллов.
Методичка по финансовой математике
Задачи с ответами для самостоятельного решения и самопроверки,
предлагаемые авторами ЕГЭ на экзаменах прошлых лет, а также из открытого банка ФИПИ:
1. 2021 год. Демонстрационный вариант ЕГЭ. Критерии здесь 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей. Решение здесь здесь
ИЛИ
Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года? Решение здесь
1. 2021 год. Вариант 1 ЕГЭ. Ященко, условие здесь Решение здесь
2. 2021 год. Вариант 7 ЕГЭ. Ященко, условие здесь Решение здесь
3. 2021 год. Вариант 11 ЕГЭ. Ященко, условие здесь Решение здесь здесь
4. 2021 год. Вариант 17 ЕГЭ. Ященко, условие здесь Решение здесь
5. 2021 год. Вариант 21 ЕГЭ. Ященко, условие здесь Решение здесь здесь
6. 2021 год. Вариант 27 ЕГЭ. Ященко,условие здесь Решение здесь
7. 2021 год. Вариант 31 ЕГЭ. Ященко, условие здесь Решение здесь
8. 2020 год, основная волна, Санкт-Петербург. В июле 2026 года планируется взять кредит в банке на пять лет в размере S тыс рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле 2027, 2028 и 2029 долг остаётся равным S тысяч рублей;
— выплаты в 2030 и 2031 годах равны по 360 тысяч рублей;
— к июлю 2031 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Дублирует задание из основной волны ЕГЭ 2016 года. Решение здесь
9. 2020 год, основная волна, Москва. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму будет взят кредит в банке, если известно, что кредит будет выплачен тремя равными платежами (за 3 года) и общая сумма выплат будет на 78 030 рублей больше суммы взятого кредита. Решение здесь или здесь + здесь
10. 2020 год, основная волна, Краснодар. В кредит взяли 220 тыс. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трех лет задолженность остается неизменной и равной 220 тысячам рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен. Найдите r если известно, что сумма всех выплат составит 420 тысяч рублей. Решение здесь
11. 2020 год, досрочная волна. В июле планируется взять кредит в банке на сумму 10 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 15 млн рублей? Решение здесь + здесь + здесь
12. 2020 год. Вариант 1 ЕГЭ. Ященко условие здесь Решение здесь Критерии здесь
13. 2020 год. Вариант 7 ЕГЭ. Ященко условие здесь здесь Решение здесь Критерии здесь
14. 2020 год. Вариант 11 ЕГЭ. Ященко условие здесь Решение здесь Критерии здесь здесь
15. 2020 год. Вариант 17 ЕГЭ. Ященко условие здесь Решение здесь здесь Критерии здесь
16. 2020 год. Вариант 22 ЕГЭ. Ященко условие здесь Решение здесь Критерии здесь
17. 2020 год. Вариант 27 ЕГЭ. Ященко условие здесь Решение здесь Критерии здесь
18. 2020 год. Вариант 31 ЕГЭ. Ященко условие здесь Решение здесь Критерии здесь
19. 2019 год. Основная волна ЕГЭ. Центр. В июле планируется взять кредит в банке на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите x, если известно, что за весь период выплатили на 15% больше, чем взяли в кредит.
20. 2018 год, основная волна. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата
таковы:
– в январе каждого года долг увеличивается на 20% по сравнению с предыдущим годом;
– с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен четырьмя равными платежами (то есть за четыре года) и общая сумма выплат составила 311040 рублей. Решение здесь
21. 2018 год, основная волна. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата
таковы:
– в январе каждого года долг увеличивается на 25% по сравнению с предыдущим годом;
– с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен тремя равными платежами (то есть за 3 года) и общая сумма выплат на 65500 рублей больше суммы кредита.
Решение здесь
22. 2018 год, основная волна. В регионе А среднемесячный доход на душу населения в 2014 году составлял 43740 рублей и ежегодно увеличивался на 25%. В регионе В среднемесячный доход на душу населения в 2014 году составлял 60000 рублей. В течение трех лет суммарный доход жителей региона увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах А и В стал одинаковым. Найдите m. Решение здесь здесь
23. 2018 год,основная волна. 15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего
месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 20-й долг должен быть на 30 тысяч рублей меньше
долга на 15-е число предыдущего месяца;
– к 15-му числу 21-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его
погашения составит 1604 тысячи рублей? Решение здесь здесь
24. 2018 год,основная волна. 15 января планируется взять кредит в банке на некоторую сумму на 11 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
– 15-го числа каждого месяца с 1-го по 10-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
– 15-го числа 10-го месяца долг составит 300 тысяч рублей;
– к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1388 тысяч рублей? Решение здесь здесь
25. 2018 год,основная волна. 15 декабря планируется взять кредит в банке на 1 000 000 рублей на (n+1) месяц. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
- cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
-15-го числа n-го месяца долг составит 200 тысяч рублей;
- к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составить 1378 тысяч рублей. Решение здесь здесь
26. 2018 год,основная волна. 15 января планируется взять в банке кредит в 700 тыс. руб. на (n+1) месяц. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на 1% по сравнению с концом предыдущего месяца;
- cо 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
– 15-го числа каждого с 1-го по n-й месяц долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца ;
- за n+1 месяц кредит должен быть полностью погашен.
Найдите n, если банку всего было выплачено 755 тыс. руб., а долг на 15-е число n-го месяца составлял 300 тыс. руб. Решение здесь
27. 2018 год,основная волна. Зависимость количества Q (в шт., ) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q = 15000 - P. Затраты на производство Q единиц товара составляют 3000Q + 1000000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0 < t< 1000) с каждой произведенной единицы товара. Таким образом, прибыль фирмы составляет PQ - 3000Q - 1000000 - tQ рублей, а общая сумма налогов, собранных государством, равна tQ рублей. Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной? Решение здесь здесь
28. 2018 год,основная волна. Зависимость объёма Q (в шт.) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q = 15000 - P,
Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q + 5000000 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли? Решение здесь
29. Задача на вклады. Вкладчик внес в банк 500000 рублей под 20% годовых. В конце каждого года из первых трех лет после начисления процентов он дополнительно вносил одну и ту же сумму. К концу четвёртого года его вклад стал равным 1364400 рублей. Какую сумму в рублях дополнительно вносил вкладчик в течении каждого из первых трех лет? Решение здесь
30. Финансовая задача на оптимальный выбор. В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей? Решение здесь
31. Задача на вклады.
Ответ здесь
Вклады здесь
32. Вкладчик открыл счёт в банке, разместив сумму 120 000 рублей под 10% годовых. Какая сумма будет на счете через 3 года?
Решение здесь
33. Вкладчик открыл счёт в банке на 4 года, разместив сумму в размере 160 000 рублей. Чему равна годовая процентная ставка в банке, если через 4 года (после 4 начислений) сумма на его счете равна 194 481.
Решение здесь
34. Вкладчик положил в банк 1000 000 рублей под 10% годовых на 3 года (проценты начисляются один раз после истечения каждого года) с правом докладывать три раза (в конце каждого года до начисления процентов) на счёт фиксированную сумму 133 000 рублей. Какая сумма будет у вкладчика через 3 года?
Решение здесь
Примеры здесь и здесь и здесь и здесь и здесь и здесь и здесь
Кредиты здесь
Дифференцированный платеж здесь
Основные характеристики дифференцированного платежа здесь
Задача здесь и здесь Задача здесь и здесь Задача здесь Задача здесь Задача здесь
Задача здесь и здесь Задача здесь и здесь
Аннуитетный платеж здесь и здесь
Задача здесь Задача здесь Задача здесь Задача здесь
Равные платежи, кроме последнего здесь
Задачи на таблицы здесь и здесь Задача здесь Задача здесь Задача здесь Задача здесь
Разные платежи здесь Задача здесь Задача здесь Задача здесь и здесь Задача здесь и здесь Задача здесь и здесь Задача здесь и здесь
Задачи на оптимальный выбор. Исследование функций.
Производная элементарных функций здесь
Производная сложной функции здесь
Правила нахождения производной здесь
Геометрический смысл производной здесь
Физический смысл производной здесь
Нахождения наибольшего и наименьшего значения квадратичной функции здесь
Нахождение наибольшего и наименьшего значения функции здесь
Теорема о единственном экстремуме здесь
Нахождения наибольшего и наименьшего значения функции натурального аргумента здесь и здесь
Поиск чисел здесь
Задача здесь Задача здесь Задача здесь
Геометрические задачи здесь
Задача здесь Задача здесь Задача здесь Задача здесь
Прямоугольная система координат здесь
Задача здесь и здесь Задача здесь Задача здесь
Задача здесь и здесь Задача здесь Задача здесь Задача здесь
Задача здесь и здесь Задача здесь и здесь Задача здесь Задача здесь
Задачи ЕГЭ 3 здесь
Задача здесь Задача здесь Задача здесь
Чтобы продолжить подготовку к ЕГЭ 2021, перейдите по ссылкам на другие страницы сайта:
ЛокацияГлавная страница Карта сайта
Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail: [email protected]
2. У Царя Гороха было три сына. Среди потомков Царя Гороха десять имели каждый ровно по два сына, а у остальных детей не было вообще. Сколько потомков было у царя Гороха?Замечание: Дочерей ни у кого не рождалось.
2А.Задача-аналог. У Царя Гвидона было 5 сыновей. Среди его потомков 100 имели каждый ровно по 3 сына, а остальные умерли бездетными. Сколько потомков было у царя Гвидона?
Подсказка. При подсчете потомков не забудьте о сыновьях Гвидона
Решение. Всякий потомок Царя Гвидона - это либо сын одного из его потомков, либо сын самого Гвидона. Из условия следует, что у всех потомков Гвидона было в общей сложности 100·3=300 сыновей. А у самого Гвидона было 5 сыновей, следовательно, всего потомков было 305. Ответ: 305.
5. Из Ливерпульской гавани каждое утро в 9.00 выходит кораблик в Бразилию. Также каждое утро в 9.15 кораблик из Бразилии выходит и плывет по тому же маршруту в Ливерпуль. Дорога из Ливерпуля в Бразилию, также как и дорога из Бразилии в Ливерпуль, занимает у кораблика ровно 10 суток. Сегодня, как обычно, по расписанию из Ливерпуля выплыл кораблик "Дон". Сколько корабликов из Бразилии встретит "Дон", пока он плывет по назначению?
5А.Задача-аналог.
Каждый день в полдень из Гавра в Нью-Йорк отправляется пароход, и в тот же самый момент пароход той же компании отправляется из Нью-Йорка в Гавр. Переезд совершается ровно за 7 суток как в том, так и в другом направлении. Сколько судов своей компании, идущих в противоположном направлении, встретит пароход, отправляющийся сегодня в полдень из Гавра? (Это задача французского математика 18 века Э. Люка. Она просто решается применением графика).
Ответ: 15 пароходов.
Решение ясно из рисунка
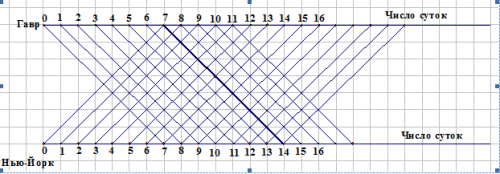
Пароход, график движения которого изображен жирной линией, встретит в океане 13 пароходов, да один при выходе из Гавра, да еше один , готовый к отплытию , в порту Нью-Йорка, т. е. он встретит 7 пароходов, вышедших в течение 7 дней до его отправления, 7 пароходов , вышедших в течение его плавания, да пароход, отправляющийся в путь в момент его прибытия в Нь-Йорк. Все встречи, как видно из графика, происходят в полдень и в полночь.
1. Костин дедушка очень любит давать Косте задачи на числа. Вот одна из его задач: «Произведение двух последовательных натуральных чисел равно 210. Найди эти числа».
Решение. 210 = 2·3·5·7 = (2·7)·(3·5) = 14·15. Ответ: 14 и 15.
1А.Бабушка Аня спрашивает у внучки, какие два последовательных натуральных числа надо перемножить, чтобы получить 462? Помогите внучке ответить на вопрос бабушки.
Решение. 462 = 2·3·7·11= (2·11)·(3·7) = 21·22. Ответ: 21 и 22.
1Б.Дед Бародед придумал задачу: «Произведение каких двух последовательных натуральных чисел равно 1122?» Решите дедушкину задачу. Решение. 1122 = 2·3·11·17 = (2·17)·(3·11) = 33·34. Ответ: 33 и 34.
1В. Учитель предложил учащимся 5 класса найти такие два последовательных натуральных числа, чтобы их произведение равнялось 1482. Какой же ответ ожидал услышать учитель?
Решение. 1482 = 2·3·13·19 = (2·19)·(3·13) = 38·39. Ответ: 38 и 39.
2. Вчера Луиза купила 9 бубликов, 6 булочек, 12 яиц (по 15 центов каждый).Ей также было нужно молоко, и она купила 3 литровых пакета молока.Когда кассирша выдала ей чек на $8,65, Луиза попросила проверить счет.Как Луиза догадалась, что кассирша ошиблась?
Решение. Заметим, что количество каждого вида товара, купленого Луизой, делится на 3.Отсюда вывод: стоимость всего товара, независимо от цены отдельного товара, тоже должна делится на 3.А это значит, что сумма цифр числа 8,65 (суммы всех товаров) должна делиться на 3, а она не делится (8+6+5=19 , 19 на 3 не делится).
Поэтому внимательная девочка Луиза попросила проверить счет.
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка инстаграм