Демоверсия ОГЭ
Локация Главная страница Карта сайта
Официальная демоверсия ОГЭ по математике от ФИПИ на 2021 год.
Изменения в КИМ 2021 года по сравнению с 2020 годом
В рамках усиления акцента на проверку применения математических знаний в различных ситуациях количество заданий уменьшилось на одно за счет объединения заданий на преобразование алгебраических (задание 13 в КИМ 2020 г.) и числовых выражений (задание 8 в КИМ 2020 г.) в одно задание на преобразование выражений на позиции 8 в КИМ 2021 г.
Задание на работу с последовательностями и прогрессиями (задание 12 в КИМ 2020 г.) заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях (задание 14 в КИМ 2021 г.).
Скорректирован порядок заданий в соответствии с тематикой и сложностью.
Максимальный первичный балл уменьшен с 32 до 31.
Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.
Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы,а затем перенесите в бланк ответов № 1. Если получилась обыкновенная дробь, ответ запишите в виде десятичной.
Решения заданий части 2 и ответы к ним запишите на бланке ответов № 2. Задания можно выполнять в любом порядке. Текст задания переписывать не надо, необходимо только указать его номер.
Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки.
Сначала выполняйте задания части 1. Начать советуем с тех заданий,которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время,Вы сможете вернуться к пропущенным заданиям.
При выполнении части 1 все необходимые вычисления,преобразования выполняйте в черновике. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом КИМ, и линейкой.
Баллы, полученные Вами за выполненные задания, суммируются.Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2 баллов должны быть получены за решение заданий по геометрии (задания 15–19, 23–25).
После завершения работы проверьте, чтобы ответ на каждое задание в бланках ответов № 1 и № 2 был записан под правильным номером.Желаем успеха!
Демонстрационная версия ОГЭ по математике. 9 класс. ФИПИ. 2021 год.
ЧАСТЬ 1
Ответами к заданиям 1–19 являются число или последовательность цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
1-5. Комментарий. Комплексное задание на использование приобретённых знаний математики в практической деятельности и повседневной жизни, состоит из пяти подзадач. В таком виде оно предложено впервые в прошлом учебном (2019-2020) году. Чтобы решить задачу нужно несколько раз внимательно прочитать текст под чертежом и выделить ключевую информацию. Не забывайте, что на рисунке непосредственно в тексте работы можно делать отметки и выполнять необходимые Вам построения. Внимание: при решении этих заданий главное анализировать чертеж совместно с текстом, который его объясняет. Здесь вы можете посмотреть логику и последовательность решения каждого из пяти заданий.
Прочитайте внимательно текст и выполните задания 1–5.
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.
Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
2. Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Комментарий. Так же, как в первой задаче внимательно изучаем текст и план, чтобы определиться сначала с общим количеством плитки, а затем с упаковками.
3. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Комментарий. Решив первые две задачи, мы уже определились с тем, какая фигура на плане обозначает жилой дом. В нашем случае это пятиугольник. Чтобы вычислить его площадь нужно мысленно "разрезать" его на более простые фигуры (здесь можно на прямоугольники) или, наоборот, "склеить" из них. Строго говоря, воспользоваться свойством аддитивности площади.
4. Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
Комментарий. Сначала подумайте и отметьте на плане дома точку, ближайшую к гаражу, и на плане гаража - точку, ближайшую к дому. Соедините эти точки прямой линией с помощью линейки. Если построенная прямая не совпадает с линиями сетки, т.е. наклонна по отношению к ним, то придётся воспользоваться теоремой Пифагора.
5. Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котел) | Прочее оборудование и монтаж | Сред. расход газа / сред. потребл. мощность | Стоимость газа / электро-энергии | |
| Газовое отопление | 24 тыс. руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 тыс. руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт·ч ) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Комментарий 1. Задачи с условием в виде таблицы встречались в разные годы как в ЕГЭ по математике обоих уровней, так и в ОГЭ. Бывали варианты, когда достаточно только сравнить табличные значения, чтобы выбрать нужное. Бывали варианты, когда требовалось провести дополнительные вычисления. Представленная здесь задача относится к последнему типу. Такие задачи лучше всего решать добавлением в таблицу столбиков с промежуточными результатами. Это позволяет лучше структурировать данные и облегчает их последующий анализ и выбор ответа.
Комментарий 2. При выполнении арифметических действий следите за размерностями табличных данных. Складывайте рубли с рублями и умножайте киловатты на их стоимость.
Комментарий 3. Для тех, кому интересно: 500 часов = 500/24 ≈ 20,83 суток, т.е. затраты окупятся меньше, чем за месяц.
6. Найдите значение выражения
Решение Комментарий 1 Комментарий 2. Такое же задание вы встретите и на ЕГЭ за 11 класс в варианте базового уровня под № 1
7. На координатной прямой отмечена точка А.

Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А?
1)
2)
3) 0,6
4) 4
Решение Комментарий 1 Комментарий 2. Аналогичное задание в ЕГЭ базового уровня встретите под № 17. Усложнение состоит в том, что среди проверяемых чисел могут оказаться значения пока неизвестных вам показательной и логарифмической функций.
8. Найдите значение выражения при a = 5.
9. Решите уравнение
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Решение Комментарий 1 Комментарий 2. Девятиклассники найдут свои уравнения на странице сайта, посвященной решению простейших уравнений.
10. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Решение Комментарий. В этом задании ОГЭ по математике чаще всего встречаются задачи на применение классического определения вероятности и на основы комбинаторики. Этим же темам посвящены задачи базового уровня ЕГЭ. Пройдите по ссылке и вы найдете еще материалы по теме "Теория вероятностей".
11. Установите соответствие между графиками функций и формулами, которые их задают.
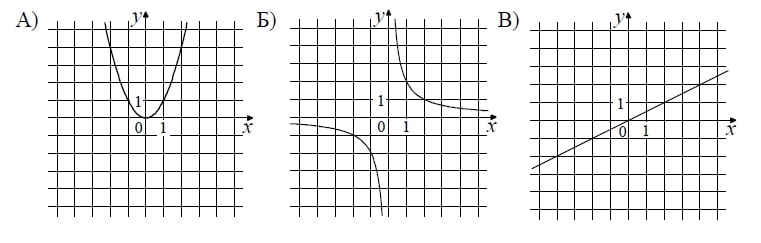
1)
2)
3)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А | Б | В |
Решение Комментарий. В этом задании могут быть различные вопросы, связанные с анализом и сравнением графиков линейной, квадратичной, степенной и дробно-рациональной функций. Повторите свойства этих графиков.
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой tF = 1,8tC + 32, где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует −25 градусов по шкале Цельсия?
Решение Комментарий Проверьте себя на аналогичных заданиях 4 базового уровня ЕГЭ.
13. Решите систему неравенств
На каком рисунке изображено множество её решений?

1) 1
2) 2
3) 3
4) 4
14. Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика на пятый день?
Решение Комментарий 1 Комментарий 2. Необходимые формулы можно найти в разделе Справки

15. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.
16. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.
17. Найдите площадь трапеции, изображённой на рисунке.
18. Найдите тангенс острого угла, изображённого на рисунке.
19. Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы. Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
ЧАСТЬ 2
При выполнении заданий этой части вам нужно будет записать полное решение задачи на отдельном листе. И оцениваться будет именно решение. При выполнении заданий 20–25 используйте БЛАНК ОТВЕТОВ № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
20. Решите уравнение
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учётом дальнейшие шаги выполнены верно | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
21. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Правильно составлено уравнение, получен верный ответ. | 2 |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа. | 1 |
| Другие случаи, не соответствующие указанным критериям. | 0 |
| Максимальный балл | 2 |
22. Постройте график функции и определите, при каких значениях параметра с прямая y = c имеет с графиком ровно одну общую точку.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| График построен правильно, верно указаны все значения c, при которых прямая y = c имеет с графиком только одну общую точку. | 2 |
| График построен правильно, указаны не все верные значения c. | 1 |
| Другие случаи, не соответствующие указанным критериям. | 0 |
| Максимальный балл | 2 |

23. В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6 , BC = 8 . Найдите медиану CK этого треугольника.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ. | 2 |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. | 1 |
| Другие случаи, не соответствующие указанным критериям. | 0 |
| Максимальный балл | 2 |
24. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Доказательство верное, все шаги обоснованы. | 2 |
| Доказательство в целом верное, но содержит неточности. | 1 |
| Другие случаи, не соответствующие указанным критериям. | 0 |
| Максимальный балл | 2 |
25. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ. | 2 |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. | 1 |
| Другие случаи, не соответствующие указанным критериям. | 0 |
| Максимальный балл | 2 |
Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания.
Поделитесь со своими друзьями в социальных сетях ссылкой на сайт vivat2.okis.ru
Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail: [email protected]
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка лайков вк