№3 и 6 ЕГЭ профиль / vivat2.okis.ru

Меню

№3 и 6 ЕГЭ профиль

Математика - это здорово!

Основы геометрии: задания № 3 и № 6 ЕГЭ профиля математики

1. На клетчатой бумаге с размером клетки 1 х 1 изображён угол. Найдите тангенс этого угла.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

2. На клетчатой бумаге с размером клетки 1 х 1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

3. На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите длину отрезка AB.

Подсказка здесь Ответ здесь

4. В треугольнике ABC угол C равен 90°, sinA=3/5, AC=4 Найдите AB.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

5. В треугольнике ABC угол C равен 90°, tgA=0,5 ВС = 4. Найдите АС.

Подсказка здесь Ответ здесь

6. В треугольнике ABC угол C равен 90°, AB=13, tgA=8. Найдите высоту CH.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

7. В треугольнике АВС угол С равен 90°, CH — высота, BC=3, sinA=1/6. Найдите АН.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

8. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

9. На клетчатой бумаге с размером клетки 1 см × 1 см изображён треугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

10. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Подсказка здесь Ответ здесь

11. На клетчатой бумаге с размером клетки 1 см х 1 см изображено кольцо. Найдите его площадь. В ответ запишите площадь, делённую на . Ответ дайте в квадратных сантиметрах.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

12. На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

13. На клетчатой бумаге изображен круг площадью 48. Найдите площадь заштрихованного сектора.

Подсказка здесь Ответ здесь

14. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Ответ здесь

15. В треугольнике ABC AC = BC, AB = 9,6, sinA = 7/25. Найдите AC.

Подсказка здесь Ответ здесь или здесь

16. В треугольнике ABC AC = BC = 8, cosA = 0,5 Найдите АВ.

Подсказка здесь Ответ здесь

17. В треугольнике ABC, AC = BC, AB = 5, cos∠BAC = 7/25. Найдите высоту AH.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

18. В треугольнике ABC AC + BC = 30, AH — высота, cosBAC = 2/5. Найдите BH.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

19. В треугольнике ABC AC = BC = 2√2, угол C равен 135°. Найдите высоту AH.

Подсказка здесь Ответ здесь

20. В треугольнике АВС АС = ВС = 2√3, угол С равен 120° Найдите высоту АН.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

21. В треугольнике ABC угол C равен 90°, СН — высота, BC = 3, cosA = √35/6. Найдите АН.

Подсказка здесь Ответ здесь

22. В треугольнике ABC угол C равен 90°, высота CH равна 10, BH = 5√21. Найдите cosA.

Подсказка здесь Ответ здесь

23. Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (8; 4), (8; 8), (2; 10).

Подсказка здесь здесь Ответ здесь

24. Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (10; 4), (10; 10), (2; 6).

Ответ здесь

25. В параллелограмме ABCD AB = 2, AD = 9, sinA = 4/9 Найдите большую высоту параллелограмма.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

26. Площадь прямоугольника равна 54. Найдите его большую сторону, если она на 3 больше меньшей стороны.

Подсказка 1 здесь Ответ здесь

27. Найдите периметр прямоугольника, если его площадь равна 272, а отношение соседних сторон равно 4 : 17.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

28. Периметр прямоугольника равен 54, а диагональ равна 26. Найдите площадь этого прямоугольника.

Подсказка здесь Ответ здесь

29. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.

Подсказка 1 здесь Подсказка 2 здесь Ответ здесь

30. Диагонали ромба относятся как 1 : 9. Периметр ромба равен 164. Найдите высоту ромба.

Ответ здесь

31. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции

Ответ здесь

32. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.

Ответ здесь

33. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции

Ответ здесь

34. Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Ответ здесь

35. Основания трапеции равны 6 и 8. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Ответ здесь

36. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 19, отсекает треугольник, периметр которого равен 39. Найдите периметр трапеции.Ответ здесь

37. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 46. Найдите ее среднюю линию

Ответ здесь

38. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах

Подсказка здесь Ответ здесь

39. Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах

Ответ здесь

40. Дуга окружности AC, не содержащая точки B, составляет 210°. А дуга окружности BC, не содержащая точки A, составляет 30°. Найдите вписанный угол ACB. Ответ дайте в градусах.

. Ответ здесь

41. Угол ACB равен 3° Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

Подсказка здесь Ответ здесь

42. Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 28

Ответ здесь

43. Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса 22√3

Подсказка здесь Ответ здесь

44. Хорда AB стягивает дугу окружности в 70°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах

Ответ здесь

45. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника

Ответ здесь

46. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь

Подсказка здесь Ответ здесь

47. Около окружности описана трапеция, периметр которой равен 84. Найдите длину её средней линии

Ответ здесь

48. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного треугольника

Подсказка 1 здесь Подсказка 2 здесь Подсказка 3 здесь Ответ здесь

49. Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1 : 8 : 9. Найдите больший угол треугольника ABC. Ответ дайте в градусах

Ответ здесь

50. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол B этого четырехугольника. Ответ дайте в градусах

Ответ здесь

51. В треугольнике ABC AC = 4, BC = 3, угол C равен 90°. Найдите радиус описанной окружности этого треугольника

Ответ здесь

52. Около трапеции описана окружность. Периметр трапеции равен 48, средняя линия равна 19. Найдите боковую сторону трапеции

Ответ здесь

53. В треугольнике ABC угол C равен 90°, CH – высота, угол A равен 30°, AB = 4 Найдите BH.

Ответ здесь

54. Найдите периметр прямоугольника, если его площадь равна 176, а отношение соседних сторон равно 4 : 11

Ответ здесь

55. Около окружности описана трапеция, периметр которой равен 84. Найдите длину её средней линии

Ответ здесь

56. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол B этого четырехугольника. Ответ дайте в градусах

Ответ здесь

57. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры.

Ответ здесь

58. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Ответ: здесь

Прямая ссылка на встроенное изображение

Заочный кружок1-4 класса Математический кружок для дошкольников Олимпиадные задания по математике 3 класс Математика онлайн для начальной школы Сложение и вычитание

Задача 1 . Где жил Боря ?

Алик, Боря и Вова жили в разных домах.

Два дома были в два этажа, один дом был одноэтажный.

Алик и Боря жили в разных (по количеству этажей) домах, Боря и Вова также жили в разных (по количеству этажей) домах.

Где жил Боря ?

Дома

(a) А; (b) Б; (c) В.

Решение.

Какие мальчики живут в разных с Борей домах ?

Это Алик и Вова.

Сколько домов должно отличаться от домика Бори ? Два.

А какой у нас есть домик, который отличается от двух других ?

Конечно же одноэтажный домик отличается от двух двухэтажных домиков.

Вот в нем и должен жить Боря.

Задача 2. Кто лишний ?

Вы , наверное сразу заметили, что здесь есть " лишняя" мордашка!

А теперь вглядитесь внимательно во все рисунки.

Сколько вариантов "лишних" рисунков Вы заметили ?

Рожицы

(a) 1; (b) 2; (c) 3; (d) 4; (e) 5; (f) 6.

Решение

Правильный ответ - "e".

Сколько признаков мы видим у каждой мордашки ?

форма носика;

форма ротика;

форма глаз и бровей;

форма ушек;

есть на голове котелок или нет.

А теперь поищем "лишние" мордашки:

Есть ли мордашка, отличающаяся от всех по форме носика ?

Первая мордашка: носик - треугольник, повернутый книзу, а у всех - кверху;

Есть ли мордашка, отличающаяся от всех по форме ротика ?

Вторая мордашка: ротик расплылся в улыбке, а у всех - строгое лицо, без улыбки;

Есть ли мордашка, отличающаяся от всех по форме глаз и бровей ?

Третья мордашка: глаза - продолговатые, брови -длинные, а у всех глаза - круглые, брови- короткие.

Есть ли мордашка, отличающаяся от всех по форме ушек ?

Пятая мордашка: ушки оттопыренные, а у всех - ровные.

Есть ли мордашка, отличающаяся отсутствием или наличием котелка ?

Четвертая мордашка: - без котелка, а у всех - котелок;

Всего можно насчитать пять лишних мордашек.

Задача 3. Играем в слова

Маша очень любит игру со словами. Она и для вас приготовила такую игру:

Машин пример

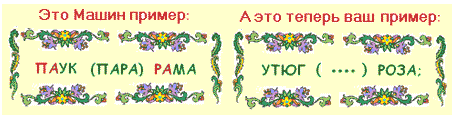
Поставьте вместо точек - новое слово, но сначала посмотрите, как это сделала Маша.

Если вы уже догадались, поищите свое слово в списке ответов:

(a) утка; (b) рама; (c) рыба; (d) утро;

Решение.

Правильный ответ - "d". Построенное слово - утро.

Маша из двух слов построила новое слово : пара.

Какой слог она взяла от своего первого слова ? Первый !

А какой слог мы возьмем от нашего первого слова ? Тоже первый - слог "ут".

А какой слог Маша взяла от своего второго слова ? Первый !

А какой слог мы возьмем от нашего второго слова ? Тоже первый - слог "ро".

Какое слово у нас получилось ? "Утро."

Что можно про него сказать ?

Что оно логически также связано со словами "утюг , роза" как слово "пара" (в Машином примере) со словами "паук, рама".

Учимся устанавливать логические связи и действовать по аналогии.

Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка подписчиков инстаграм

KISS

Есть известный принцип, применяемый в программировании и дизайне. По-английски он звучит так: «Keep it simple,stupid!» (Не усложняй, чудило!)

Задачи 3232 - 3238 проекта "Матема"

3232. На ветке сидят 3 птицы. Все, кроме двух, вороны, все, кроме двух, воробьи, все, кроме двух,голуби. Сколько ворон, воробьёв и голубей сидят на ветке?

3233.Катя составила из цифр 1, 2, 3, 4, 5 самое большое трёхзначное и самое маленькое двузначное числа (при этом цифры в числах не повторяются), а потом записала их разность.Какое число записала Катя?

3234.27 октября 2016года у Маши родился братик Ваня. Сегодня ему исполнился 1 месяц. Какой сегоднядень недели, если 27 октября был четверг, а в октябре 31 день?

3235.Катя позвала подруг в гости. Таня решила, что пойдёт в гости к Кате, если пойдут Оля и Марина. Оля решила, что пойдёт в гости к Кате, если пойдёт Марина. Марина решила, что пойдёт в гости к Кате, если не пойдёт Оля и пойдёт Таня. Кто из девочек пойдёт в гости к Кате?

3236.Петух Петя в течение недели с 4 до 8 утра каждые полчаса по 3 раза кричал «кукареку». Сколько всего раз Петя крикнул «кукареку» за неделю?

3237.В классе 24 ученика. Половина из них девочки. Треть всех учеников пойдут сегодня вечером в кино. Известно, что 5 из них – мальчики, а остальные – девочки. Сколько девочек не пойдут сегодня в кино?

3238.По стеблю цветка ползёт гусеница. Она начала движение в понедельник в 10 часов утра. В четверг в это же время она оказалась на высоте 42 см от земли. На какой высоте окажется гусеница в воскресенье в 10 часов утра, если известно, что во вторые сутки она поднималась вдвое быстрее, чем в первые, в третьи – вдвое быстрее, чем во вторые, и так далее.

Задача 3225 - 3231 проекта "Матема"

3225.Решите уравнение $(x^{2} - x + 1)^{2} - 10 (x - 4) (x + 3) - 109 = 0$ . В ответе укажите сумму его корней.

3226.Число aa при делении на 7 дает в остатке 2 или 4. В каком из этих случаев будет больше остаток от деления числа a^2 на 7? В ответе укажите номер правильного ответа: 1 - если число aa при делении на 7 дает в остатке 2; 2 - если число aa при делении на 7 дает в остатке 4.

3227.Два пешехода должны выйти навстречу друг другу из двух пунктов, расстояние между которыми 20 км. Если первый выйдет на полчаса раньше второго, то он встретит второго пешехода через 2,5 ч после своего выхода. Если второй выйдет на 1 ч раньше первого, то он встретит первого пешехода через 2 ч 40 мин после своего выхода. Какова скорость первого пешехода (в км/ч)?

3228.Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495. Сумма цифр этого трехзначного числа равна 17, а сумма квадратов его цифр равна 109. Найти такое трехзначное число.

3229.При каких значениях параметра b корень уравнения 6−3b+4bx=4b+12x меньше 1?

3230.Диагональ равнобедренной трапеции является биссектрисой острого угла, а основания относятся как 1:2. Периметр трапеции равен 90. Найдите большую сторону трапеции.

3231.Четырехугольник PQRS вписан в окружность. Диагонали PR и QS перпендикулярны и пересекаются в точке M. Известно, что PS=13, QM=10, QR=26. Найти площадь четырехугольника PQRS.

Задачи 3218 - 3 224 проекта "Матема"

3218.Через 52 месяца Майе исполнится ровно 7 лет. Сколько лет и сколько месяцев сейчас Майе?

3219.Пилот Саша получил задание перевезти 19 пассажиров с аэродрома Дракино на аэродром Конаково. Он запустил вертолёт на аэродроме Дракино и готов начать перевозку. Сколько посадок придётся сделать вертолёту, чтобы справиться с задачей, если всего он вмещает 5 человек, включая пилота?

3220. Маша собиралась с родителями на море. Она достала свой чемодан и поняла, что забыла код. Она помнит, что код состоит из цифр 2, 5 и 6 и что они не повторяются, но не может вспомнить их порядок.Каково максимальное количество времени, которое понадобится Маше, чтобы подобрать код,если на проверку одного кода у неё уходит 10 секунд?

3221.Аня шила платки.Сначала она разрезала ткань на 27 одинаковых квадратов, затем решила одну треть квадратов разрезать ещё на 4 части, чтобы получились носовые платочки. Из другой трети квадратов Аня сшила платки побольше, а последнюю треть квадратов она решила разрезать на 2 части и сделать шарфики. Сколько платков (носовых платков и платков побольше) и сколько шарфиков сшила Аня?

3222.У царя Додона есть роскошный сад прямоугольной формы. Злой колдун за одну ночь уменьшил сад царя Додона в 9 раз. Царь в отчаянии! А можешь ли ты сказать царю, как изменились длины сторон его сада?

3223.Встретились два кота. Кот Вася говорит: «Я за 5 недель наловлю 10 килограммов рыбы». А кот Филя отвечает: «А я наловлю столько же рыбы за 2 недели».За сколько дней они вместе наловят 10 килограммов рыбы?

3224.На школьном празднике Маша, Катя и Таня раздавали ученикам билеты в театр. Маша раздала половину всех билетов и ещё 2, Катя – половину оставшихся билетов, а Таня раздала ребятам последние 9 билетов. Сколько всего билетов раздавали ученикам на празднике?

Задача 3211 - 3217 проекта "Матема"

3211. Разность кубов двух последовательных натуральных чисел равна $331$ . Чему равен куб суммы этих чисел?

3212.При каком значении параметра a уравнение |x2−2x−3|=a имеет три корня?

3213.В трёхзначном числе зачеркнули среднюю цифру. Полученное двузначное число оказалось в 6 раз меньше исходного трёхзначного. Найдите это трёхзначное число.

3214.Стоимость билета в кино была 1200 рублей. После снижения стоимости количество посетителей увеличилось 1,5 раза и сбор увеличился на 25%. На сколько рублей была снижена стоимость билета? Дайте ответ в рублях.

3215.На часах со стрелками ровно 10. Через сколько минут стрелки часов часовая и минутная совпадут в первый раз? Дайте ответ в минутах, округлите до целых.

3216.В коробке 6 красных, 7 зелёных, 8 синих и 9 жёлтых карандашей. В темноте из коробки берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них обязательно было 3 красных и 2 зелёных карандаша?

3217.Из посёлка в город идёт автобус, и каждые 6 минут он встречает автобус, который идёт из города в посёлок, и скорость которого в 1,5 раза больше. Сколько автобусов в час приходит из города в посёлок?