Математика 6 класс
Локация Главная страница Карта сайта
Математика - это интересно! Математика - это здорово!
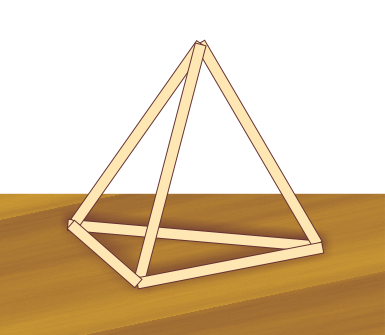
Из шести спичек можно составить четыре равных между собой равносторонних треугольника:
«Устный счёт. В народной школе С. А. Рачинского» — картина русского художника Н. П. Богданова-Бельского, написанная в 1895 году. На картине изображена деревенская школа XIX века во время урока устного счёта.


Вдоль стен квадратного бастиона комендант разместил 16 часовых по 5 человек с каждой стороны:
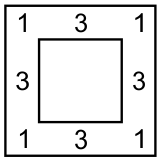
Затем пришёл полковник и распорядился поставить солдат так, чтобы с каждой стороны их было по 6:
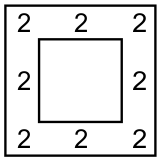
Вслед за полковником пришёл генерал и разместил солдат по 7 человек с каждой стороны:
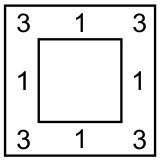
Как разрезать прямоугольник со сторонами 4 х 9 на минимальное число частей, чтобы из них сложить квадрат?
Из греческого креста (разрезав его на: а) 5 частей; б) 4 части) получаем квадрат:
Онлайн-турнир "Считай, страна!"
Пробные упражнения
Сложение и вычитание в пределах 20
Вычисления без скобок в пределах 20
Вычисления со скобками в пределах 20
Сложение в пределах 100 1 1 2 2 3 3 4 4 5 5
Вычитание в пределах 100 1 1 2 2 3 3 4 4 5 5
Таблица умножения 1 1 2 2 3 3 4 4 5 5
Умножение в пределах 100 1 1 2 2 3 3 4 4 5 5
Деление в пределах 100 1 1 2 2 3 3 4 4 5 5
Сложение натуральных чисел 1 1 2 2 3 3 4 4 5 5
Вычитание натуральных чисел 1 1 2 2 3 3 4 4 5 5
Умножение натуральных чисел 1 1 2 2 3 3 4 4 5 5
Деление натуральных чисел 1 1 2 2 3 3 4 4 5 5
Умножение и деление круглых чисел 1 1 2 2 3 3 4 4 5 5
Эффективные вычисления без скобок 11 2 2 3 3 4 4 5 5
Эффективные вычисления со скобками 1 1 2 2 3 3 4 4 5 5
Сложение десятичных дробей 1 1 2 2 3 3 4 4
Вычитание десятичных дробей 1 1 2 2 3 3 4 4
Умножение на 10; 100; .. 01,; 0,01 1 1 2 2 3 3 4 4
Умножение десятичных дробей 1 1 2 2 3 3 4 4
Деление на 10; 100; .. 0,1; 0,01 1 1 2 2 3 3 4 4 5 5
Деление десятичных дробей 1 1 2 2 4 4 5 5
Действия с десятичными дробями 1 1 2 2 3 3 4 4 5 5
Сложение обыкновенных дробей 1 1 2 2 3 3 4 4
Вычитание обыкновенных дробей 1 1 2 2 3 3 4 4
Умножение обыкновенных дробей 1 1 2 2 3 3 4 4
Деление обыкновенных дробей 1 1 2 2 3 3 4 4
Действия с обыкновенными дробями 1 1 2 2 3 3 4 4 5 5
Онлайн-турниры.Без заявок, без оплаты.
Онлайн-турнир "Думай, страна!"
Пробные упражнения
Анаграммы слов 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
Закрашенные слова 1 1 2 2 3 3 4 4 5 5
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Ребусы с картинками 1 1 2 2 3 3 4 4 5 5
Буквенные решетки 1 1 2 2 3 3 4 4 5 5
Числовые закономерности 1 1 2 2 3 3 4 4 5 5 6 6
Оригами-загадки 1 1 2 2 3 3 4 4 5 5
Опытный строитель 1 1 2 2 3 3 4 4 5 5
Опытный раскройщик 1 1 2 2 3 3 4 4 5 5
Опытный наблюдатель 1 1 2 2 3 3 4 4 5 5
Слова в таблицах 1 1 2 2 3 3 4 4 5 5
Ребусы из букв 1 1 2 2 3 3 4 4 5 5
Числовые таблицы 1 1 2 2 3 3 4 4 5 5
Закономерности в ряду фигур 1 1 2 2 3 3 4 4 5 5 6 6
Задачи и решения V олимпиады "Плюс"
Аквариум

Карусель
Все шесть рядов чисел имеют одну и ту же сумму (26)
Археолог
3023. Произведение двух взаимно простых чисел равно 1568. Чему равно наименьшее общее кратное этих чисел?
3024.На клетчатой бумаге вершина В треугольника АВС находится в одном из узлов, Если из В подняться на 5 клеток вверх и пройти 3 клетки влево, то попадем в А. Если из А пройти 3 клетки влево и опуститься на 3 клетки вниз, то попадем в С. Если площадь каждой клетки равна 1 то площадь треугольника АВС равна...
3025. На покраску (снаружи) ящика с крышкой объемом 25 л потратили 150 г краски. Сколько краски потребуется на покраску ящика объемом 200 л?
3026.Некоторый товар стоил 500 р. Цену на него увеличили на 10%, а затем уменьшили на 10%. Какой стала цена в итоге?
3027.Значение суммы 1/8 +1/24+1/48+1/80+1/120 равно...
3028.Пассажир поезда, идущего со скоростью 70 км/ч, видит проходящий встречный поезд в течение 5 с. Если длина встречного поезда равна 200 м, то его скорость равна ...
3029.На какую цифру оканчивается число 7102^2017?
3030.Стрелки часов в 12 ч 50 мин образуют угол ...
3031. Прямоугольник разделен двумя отрезками, параллельными его сторонам, на четыре прямоугольника, периметры трех из которых равны 2, 4 и 6. Периметр четвертого прямоугольника равен...
3032. Три охотника варили кашу. Один положил 2 кружки крупы, второй -1, у третьего крупы не было.Кашу же все они съели поровну. Третий охотник и говорит: "Спасибо за кашу! В благодарность я даю вам 6 патронов". Как их поделить между первыми двумя охотниками по справедливости?
3023. 1568. 3024. 10,5. 3025. 1200. 3026. 495. 3027. 5/24. 3028. 74. 3029. 2. 3030. 85. 3031.8. 3032. Первому 6, второму 0.
УСТНЫЙ СЧЕТ С НАТУРАЛЬНЫМИ ЧИСЛАМИ. 6 КЛАСС
Сложение и вычитание в пределах 20. Тренинг
Сложение в пределах 100. Тренинг
УСТНЫЙ СЧЕТ С ОБЫКНОВЕННЫМИ ДРОБЯМИ. 6 КЛАСС
Сложение обыкновенных дробей. Тренинг
Вычитание обыкновенных дробей. Тренинг
УСТНЫЙ СЧЕТ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. 6 КЛАСС
Сложение десятичных дробей. Тренинг
Онлайн-турнир "Думай, страна!" (Примеры заданий)
Анаграммы слов
Составьте из букв слова, обозначающие рыб.
| б о а л в | вобла |
| л у а а к | акула |
| н ь о у к | окунь |
| м л а и н | налим |
| р у о г ь | угорь |
Разгадайте и запишите слова, обозначающие рыб.
Онлайн-турнир "Считай, страна!" Примеры заданий
Вычитание натуральных чисел
Вычислите и введите ответ (без калькулятора).
Задание 1
640 – 450 =
720 – 530 =
830 – 540 =
Задание 2
756 – 314 =
465 – 323 =
667 – 256 =
Задание 3
385 – 189 =
435 – 299 =
897 – 393 =
Задание 4
4000 – 341 =
5000 – 256 =
6000 – 981 =
8000 – 665 =
Задание 5
4100 – 1800 =
52000 – 29000 =
650000 – 280000 =
850000 – 180000 =
Множество и его элементы. Понятие множества является одним из основных в математике. Оно не определяется через другие. Поясним понятие множества на примерах.В окружающем мире мы часто имеем дело как с отдельными,объектами (предметами), так и с их группами. Например, ученик и класс учеников, футболист и футбольная команда, картина и коллекция картин,голубь и стая голубей, лошадь и табун лошадей и т. д. В математике набор каких-либо различных объектов, рассматриваемых как одно целое, называют множеством. Слова «класс», «команда»,«коллекция», «стая», «табун» и т. д. являются в математике синонимами слова «множество».Объекты (предметы), составляющие данное множество, называют его элементами.В приведенных выше примерах элементами соответствующих множеств являются ученик, футболист, картина, голубь, лошадь.
Будем обозначать множества прописными буквами латинского алфавита: А, В, С, ..., М, N, ..., а их элементы— строчными буквами: а, b, с,..., m, n, ....Элементы множества записываются в фигурных скобках в любом порядке.
Например: {13; 2; 27} и {2; 27; 13} — это одно и то же множество,состоящее из чисел 2, 13, 27. Каждый элемент записывается во множество только один раз. Например, множество букв в слове «мама» запишется: {м, а} Тот факт, что объект (предмет) а является элементом множества A,записывается а A и читается: «а принадлежит множеству A», или «а входит во множество A», «а — элемент множества A», «Множество A содержит элемент а». Запись а А означает, что а не является элементом множества A. Ее читают: «а не принадлежит множеству A», «а не является элементом множества A», или «Множество A не содержит элемента а». Например, если через N обозначить множество всех натуральных чисел, то: 5 ; 34 N;0,6 N.
Пустое множество Множество, которое не содержит ни одного элемента, называют пустым и обозначают символом Ǿ. Например, множество натуральных чисел меньших 1 не содержит ни одного элемента, поэтому оно пустое.
Примеры пустых множеств: множество букв О в слове «папа»; множество четных цифр в записи числа 157; множество натуральных чисел меньших 4-х, делящихся на 5.
Конечные и бесконечные множества Конечное множество — это такое множество, количество элементов которого конечно, т. е. такое множество количество элементов которого есть натуральное число. Множество называют бесконечным, если оно не является конечным или пустым. Например, множество корней уравнения х+28= 36, состоящее из одного числа 8 является конечным, множество букв в слове«куб» содержит 3 элемента и тоже является конечным, а множество всех натуральных чисел N и множество всех целых чисел Z— бесконечны.
Способы задания множеств Множество считается заданным, если для каждого объекта можно точно установить, является данный объект элементом данного множества или нет. Конечные множества можно задать перечислением всех их элементов.Например, если множество A состоит из чисел 2, 13, 27, то пишут: A = {2; 13; 27} и читают: «A — это множество, элементы которого —2; 13; 27». Конечные и бесконечные множества задают также описанием характеристического свойства его элементов, т. е. такого свойства, которым обладают элементы данного множества и не обладает ни один объект, не принадлежащий этому множеству. Рассмотрим, например, множество K натуральных чисел, меньших числа 6. В данном случае множество задано с помощью характеристического свойства «быть натуральным числом,меньшим числа 6». Легко перечислить элементы рассматриваемого множества: K={1; 2; 3; 4; 5}. Множество, для элементов которого указано некоторое характеристическое свойство, может быть записано так: в фигурных скобках пишут сначала обозначение элемента, после чего проводят вертикальную черту, а затем указывают характеристическое свойство. Например,множество P натуральных чисел, больших числа 10, записывается так: Р = {х| х — натуральное число, х > 10}.
Упражнения
1. Пусть A — множество дней недели, B — множество месяцев года, С — множество времен года. Запишите эти множества,применяя фигурные скобки.
2. Запишите множество букв в слове «математика».
3. Дано множество A={0,2; 33; 60}. Укажите, какие записи являются верными: 33 , 60 N, 0 N, 0 Z, 33 , 60 ,60
4. Запишите множество, в котором: а) один элемент, б) два элемента, в) бесконечное множество элементов.
5. Пусть М — множество натуральных чисел, меньших 50,делящихся на 5, но не делящихся на 2. Используя соответствующие символы, запишите, входят ли во множество М числа: 5, 10,15, 30, 35, 40.
6. Задайте множество, перечисляя его элементы, если:а) A — множество четных однозначных чисел;б) B — множество двузначных чисел, делящихся на 10;в) С—множество натуральных чисел, меньших 10.
7. Укажите характеристическое свойство элементов множества: а) {а; е; ѐ; и; о; у; э; ю; я; ы}; б) {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}; в) {11; 13; 17; 19; 23; 29}.
8. Задайте множество путем перечисления всех его элементов:
а) {р |р — простое число и 30 <р < 50}; б) {а| а N и правильная дробь}; в) {b|b N и натуральное число};г) {х| х Z и 0
9. Сколько различных множеств можно составить из 5 различных цифр?
10. Даны множества: N, Z, A= , C= ,P= , D={d| d — натуральное число d<20} Среди данных множеств укажите: а) конечные, б) бесконечные,в) множества, заданные путем перечисления всех элементов,г) множества, заданные с помощью характеристического свойства.
Подмножество. Иногда приходится рассматривать не все множество, а только его часть(например, не все множество натуральных чисел, а только множество всех простых чисел). Вместо слов «часть множества» говорят «подмножество». Таким образом, подмножество — это любая часть множества. Например,множество натуральных чисел является частью множества целых чисел,поэтому множество натуральных чисел является подмножеством множества целых. Если любой элемент множества A принадлежит также множеству B, то множество А называется подмножеством множества В.Это записывается так: А⊂В, или B⊃А, и читается: «Множество А содержится во множестве В», или «Множество В содержит множество А». Знак ⊂ называется знаком включения. *Для наглядности употребляют изображения множеств на плоскости кругами, которые называют кругами Эйлера или диаграммами Венна. Тогда тот факт, что множество А является подмножеством множества В, показывают так: круг, изображающий множество А,находится внутри круга, изображающего множество В (рис. 1).Рис.1Если «во множестве A найдется хотя бы один элемент, не принадлежащий множеству B, то множество А не будет являться подмножеством множества В. Это записывается: А⊄В. Например, множество А = {0; 1; 2; 3} не является подмножеством множества В = {1; 2; 3; 4; 5}, так как О А и О В.Из определения подмножества следует, что любое множество является подмножеством самого себя, т. е. справедливо утверждение А⊂А.Договоримся считать, что пустое множество является подмножеством любого множества А: Ǿ⊂А.Таким образом, у любого непустого множества А есть, по крайней мере, два подмножества: само множество А и пустое множество Ǿ. Два множества равны, если они состоят из одних и тех же элементов.Если каждый элемент множества A является элементом множества B и,наоборот, каждый элемент множества B является элементом множества A, то множества A и В равны. Это можно записать: A=В. Например, даны AB множества A={с; т; у; л} и В= {л; у; т; с}. Они состоят из одних и тех же элементов, записанных в разном порядке, поэтому A=В.
Упражнения
1. Даны множества: A = {3; 5; 7; 9; 11}, В = {2; 5; 7; 9}, С = {7; 9; 1},D= {3} и пустое множество Ǿ. Применяя знак включения,запишите, какие из этих множеств являются подмножествами множества А.
2. Дано множество Р={а; б; с; й). Выпишите множество всех подмножеств множества Р.
3. Даны множества:A = { р |р — простое число и 10<р <20},В = {11; 13 }, С = {11; 13; 17; 19}, D= {19;23}. Задайте множество A путем перечисления всех его элементов. Выясните есть ли среди указанных множеств равные множества. Применяя знак включения, запишите, какие из множеств B,C, D являются подмножествами множества A?
4. Запишите все подмножества множества C = {12; 14; 17; 29}.5. Дано множество A = {a|a — натуральное число a<7}.Запишите все подмножества множества A.
Операции над множествами (пересечение, объединение).Вначале рассмотрим пример. Пусть A — множество натуральных делителей числа 30 и В — множество натуральных делителей числа 45: А = {1; 2; 3; 5; 6; 10; 15; 30}, В = {1; 3; 5; 9; 15; 45}.Множества A и B имеют общие элементы: 1, 3, 5 и 15, которые являются одновременно общими делителями чисел 30 и 45. Множество C={1; 3; 5; 15} — пересечение множеств A и В. Пересечением множеств A и B (обозначают A В) называется множество, состоящее из всех тех элементов, которые принадлежат одновременно каждому из них. Для нашего примера можно записать: А В =C
*Наглядно с помощью кругов Эйлера варианты пересечения множеств изображены на рисунках 2-4. А В А В = В А В = ǾРис.2 Рис. 3 Рис. 4A BА ВА В Если множества А и В не имеют общих элементов, то их называют непересекающимися, Непересекающиеся множества изображают при помощи кругов Эйлера так, как показано на рисунке 4. Рассмотрим множества A = {1; 2; 3; 5; 6; 10; 15; 30} и B = {1; 3; 5; 9;15; 45} и построим множество С ={1;2; 3; 5; 6; 9; 10; 15; 30; 45}, которое содержит все элементы множества А и все элементы множества В и не содержит никаких других элементов. Другими словами, множество C состоит из тех и только тех элементов, которые принадлежат множеству A или множеству В. Множество С={1; 2; 3; 5; 6; 9; 10; 15; 30; 45} является объединением множеств. Объединением множеств A и B (обозначают A В) называется множество, состоящее из всех тех элементов, которые принадлежат множеству А или множеству В. Для нашего примера можно записать A=С. На рисунках 5,6,7 показано (закрашено) объединение двух множеств в случаях, когда у двух множеств есть общие элементы (ри.5), все элементы одного множества B являются элементами множества A (рис.6) и в случае,когда множества не имеют общих элементов. Рис 5 Рис 6 Рис 7
Задачи на нахождение общих элементов и всех элементов заданных множеств.
Задача 1. В классе 40 учащихся. В математическом кружке занимаются 32, в кружке «Умелые руки» — 21, а в обоих кружках — 15 учеников.Сколько учащихся не занимается ни в том, ни в другом кружке?
Решение. Воспользуемся кругами Эйлера. Пусть большой круг изображает множество всех учащихся класса, а два меньших круга Aи B изображают соответственно множество всех участников математического кружка и кружка «Умелые руки» (рис. 8). Общая часть кругов A и B изображает множество всех учащихся, занимающихся в обоих кружках. Из кругов Эйлера видно, что только в математическом кружке занимается 17 человек(32— 15= 17), а в кружке «Умелые руки» — 6 человек (21-15 = 6). Можно найти число учащихся, не занимающихся, ни в одном кружке: 40-17-15-6 =40-38 = 2. Ответ: 2 ученика.BAABA B Рис 8
Задача 2. В классе 40 учащихся. Из них 26 человек играют в баскетбол,25 — занимаются плаванием, 27 — ходят на лыжах; одновременно плаванием и баскетболом занимаются 15 человек, баскетболом и лыжами —16, плаванием и лыжами — 18. Один учащийся освобожден от физкультурных занятий. Сколько учащихся занимается всеми видами спорта? Сколько учащихся занимается только одним видом спорта?
Решение. Пусть множество Б — множество учащихся, играющих в баскетбол, множество П— множество учащихся, занимающихся плаванием,и множество Л— множество учащихся, занимающихся лыжным спортом. По условию все эти три множества попарно пересекаются. Изобразим на рисунке 9 множество всех учащихся класса в виде прямоугольника, а кругами Эйлера — множества Б, П и Л. Обозначим число элементов пересечения множеств Б, П и Л через х и определим число учащихся в каждой из непересекающихся областей. Так как по условию задачи в классе 40 учащихся, то можно составить уравнение: 26 + 25 - 15 + 27 - (34 - х) + 1 = 40, откуда х = 10. Рис 9 40ЛБ2640П2516-xx18-x15-xВ615 А17
Упражнения
1. Пусть А — множество натуральных чисел, делящихся на 4, В —множество натуральных чисел, делящихся на 6. Найдите А В.
2. Найдите пересечение и объединение множеств К и М, если К —множество всех двузначных натуральных чисел, не превосходящих 20, М — множество всех нечетных натуральных чисел,не превосходящих 30.
3. Пусть А — множество всех натуральных делителей числа 20, В— множество всех натуральных делителей числа 30. Верно ли:4. а) А В = В; б) А В = А; в) А ⊂В; г) В⊂ А.
4. Какое множество является пересечением: а) множества всех натуральных чисел и множества всех целых чисел; б) множества всех четных натуральных чисел и множества всех простых чисел?
5. Начертите два треугольника так, чтобы их пересечением: а) был треугольник; б) был отрезок; в) была точка.
6. Какая фигура может получиться в пересечении треугольника и четырехугольника? Рассмотрите несколько случаев.
7. Сколько точек может оказаться в пересечении: а) прямой и окружности; б) двух окружностей?
8. В олимпиаде участвовали 54 человека. Арифметическую задачу решили 30 человек, геометрическую — 10 человек, ту и другую— 5 человек. Сколько человек: а) решили арифметическую или геометрическую задачи; б) решили арифметическую задачу и не решили геометрической задачи; в) не решили ни одной задачи?
9. В группе из 100 туристов 70 человек знают английский язык, 45— французский язык и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?
10. В классе 30 учеников. 15 детей посещают литературный кружок,11 — биологический. Из них четверо участвуют в работе обоих кружков, пятеро занимаются в литературном и математическом кружках, а трое — в биологическом и математическом. Только один ученик посещает все три кружка. Остальные занимаются в математическом кружке. Сколько всего учащихся занимаются в математическом кружке?11.На олимпиаде по математике председатель жюри провел опрос,чтобы узнать, кто из 40 участников решил задачи А, В и С.Результаты опроса оказались таковы: задачу А решили 25 учащихся, задачу В — 22, задачу С — 22, задачу А или В решили 35 учеников, А или С — 32, В или С — 31, все три задачи решили 10 учащихся. Сколько участников олимпиады решили только одну задачу? Сколько участников не решили ни одной из трех задач?
12. В отряде из 40 ребят 30 умеют плавать, 27 — играть в шахматы, и только пятеро не умеют ни того, ни другого. Сколько ребят умеют плавать и играть в шахматы?
Лист самоконтроля 7 (6 класс)
1.Как вводятся координаты на плоскости? (Вопрос 1 на ст.228)
2.У точек какой прямой координатной плоскости одинаковые: а) абсциссы; б) ординаты? (Вопрос 3 на ст.228)
3.Как найти координаты точки координатной плоскости? (Вопрос 5 на ст.228)
4.Что такое координатные углы (четверти)? Сколько их? (Вопрос 7 на ст.228)
5.Как построить по формуле график: а) прямой пропорциональности; б) обратной пропорциональности (Вопрос 2 на ст.235)
6.Запишите формулу линейной зависимости. (Вопрос 1 на ст.239)
7.Сформулируйте правило умножения: а) двух чисел разных знаков; б) двух отрицательных чисел (Вопрос 1 на ст.245)
8.Какие числа называются взаимно обратными? (Вопрос 1 на ст.254)
9.Как разделить два числа с разными (одинаковыми) знаками? (Вопрос 2 на ст.259)
10.Как найти: а) длину окружности; б) площадь круга? (Вопрос 2 на ст.263)
11.Что значит возвести число а в n-ю степень? (Вопрос 3 на ст.275)
12.Как степени с натуральными показателями: а) умножают; б) делят?(Вопрос 1 на ст.278)
13.Как возводят в степень произведение? (Вопрос 2 на ст.283)
14.Чему равна степень а с целым отрицательным показателем – n? (Вопрос 3 на ст.288)
15. Что называется биссектрисой? (Вопрос 2 на ст.25)
Лист самоконтроля 8 (6 класс)
1.Как называется первая (вторая) координата точки координатной плоскости?(Вопрос 2 на ст.228)
2.Какой вид имеют координаты точек: а) оси абсцисс; б) оси ординат; в) начала координат? (Вопрос 4 на ст.228)
3.Как построить точку по ее координатам? (Вопрос 6 на ст.228)
4.Запишите формулу: а) прямой пропорциональности; б) обратной пропорциональности. (Вопрос 1 на ст.235)
5.Как построить график линейной зависимости? (Вопрос 2 на ст.239)
6.Сформулируйте распределительный закон умножения относительно сложения. (Вопрос 2 на ст.251)
7.Как раскрываются скобки, когда перед ними стоит знак: а) «+»; б) «-»?(Вопрос 4 на ст.251)
8.Как разделить одно число на другое? (Вопрос 1 на ст.259)
9.Чему равно отношение длины окружности к длине ее диаметра? (Вопрос 1 на ст.263)
10.Как в выражении аn называются числа а и n? (Вопрос 2 на ст.275)
11.Положительное или отрицательное число получится при возведении отрицательного числа в степень: а) четную; б) нечетную? (Вопрос 5 на ст.275)
12.Как возводят степень в степень? (Вопрос 1 на ст.283)
13.Как возводят в степень дробь (частное)? (Вопрос 3 на ст.283)
14.Как называется запись u=a·10k? Какими могут быть числа: u, а, k? (Вопрос 1 на ст.292)
15.Какой треугольник называется равнобедренным? (Вопрос 2 на ст.52)
Устный счет: как научиться считать устно
Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно
И успех тебя ждет обязательно!
Шишкина школа. Математика. Видео
Mеждународный математический конкурс
Открытая интернет-олимпиада ФИЗТЕХ 2015
Число N равно произведению 200 простых чисел (не обязательно различных). Если каждый множитель в этом представлении увеличить на единицу, то полученное произведение будет делиться на N. Сколько различных таких натуральных N существует?
В каждую клетку таблицы 7×7 ставят 0 или 1. Сколькими способами это можно сделать так, чтобы сумма чисел в каждой строке и каждом столбце была четной?
Индейцы племени “Мат-и-матика” умели разрезать квадрат на прямоугольники особым образом. Они разрезали его так, чтобы любая вертикальная и горизонтальная прямая, не содержащая сторон прямоугольников разрезания, пересекала ровно 60 прямоугольников. На какое наименьшее число прямоугольников индейцы могли разрезать квадрат?
Из поселка A в поселок F ведет прямолинейная дорога длиной 35 км. Остановки автобуса расположены в поселках B, C, D и E. Известно, что AC=12 км, BD=11 км, CE=12 км и DF=16 км. Найдите расстояние EF.
В понедельник в школьную библиотеку пришло 5 учеников, во вторник — 6, в среду — 4, в четверг — 8, в пятницу — 7. Никто из учеников не был в библиотеке два дня подряд. Какое наименьшее количество учеников побывало в библиотеке с понедельника по пятницу?
Два бегуна тренируются на круговом стадионе. Они стартуют с диаметрально противоположных точек, и время от времени один из них обгоняет другого. Известно, что третий обгон произошёл после часа с начала тренировки. Через какое количество минут после третьего случился 7 обгон?
Пусть N - наименьшее натуральное число, которое дает различные остатки от деления на 2,4,…,1000. Какой остаток число N дает при делении на 1000?
В классе несколько детей, которые ходят в кружки. В каждый кружок ходит ровно 11 учеников. Каждый из учеников ходит ровно в 2 кружка. Для любых двух кружков ровно один ученик посещает оба этих кружка. Сколько учеников в классе?
В преддверии хоккейного матча “Метеор” — “Вымпел” стала известна информация о купленных билетах. На южную трибуну было продано более 7/11 билетов, на северную — более 10% билетов, на западную — более 5/19 билетов, а на восточную трибуну билетов не продавали. Какое наименьшее число билетов могло было продано на матч?
В сломанной повозке лошадь, идущая слева, устаёт через 30 км бега, а лошадь, идущая справа, – через 130 км. Через сколько километров после начала движения нужно поменять лошадей местами, чтобы они устали одновременно?
Сколькими способами можно выбрать из 11 человек группу для участия в эксперименте, состоящую из по крайней мере одного человека (в группе может быть любое число человек от 1 до 11)?
На острове живет 25 человек: рыцари, лжецы и хитрецы. Рыцари всегда говорят правду, лжецы всегда лгут, а хитрецы отвечают на заданные им вопросы по очереди то правду, то ложь. Все жителям острова было задано три вопроса: “Вы рыцарь?”, “Вы хитрец?”, “Вы лжец?”. На первый вопрос “Да” ответили 20 человек, на второй — 14 человек, на третий — 10 человек. Сколько хитрецов живет на этом острове?
Управление информационных образовательных технологий Национального института образования
Онлайн-курсы для школьников с лучшими преподавателями России
Время проведения: 19:00 - 20:00 часов 25.10.2014
Зимняя интернет-олимпиада по математике, 19-27 января 2015
Весенняя интернет-олимпиада по математике, 20-28 апреля 2015
V Дистанционная олимпиада по математике Школы точных наук ГрГУ среди учащихся 5-7 классов 2014-2015 учебного года проводится в 3 этапа
1.Некоторое число увеличили в 2,5 раза, а затем вычли половину исходного числа, после чего получили число на 4,4 больше исходного. Чему равно исходное число? |
2.Проволоку длиной метра разрезали на три части. Первая часть составила 1/4 всей проволоки, вторая – проволоки, оставшейся после того, как отрезали первую часть. Какова длина второй части? Укажите правильный вариант ответа.
1) 32 м 2) м 3) 23 м 4) м
3. Из Гродно в Скидель выехал автомобилист. Одновременно из Скиделя в Гродно выехал велосипедист. После из встречи автомобилист повернул обратно, а велосипедист продолжил свой путь. Известно, что автомобилист вернулся в Гродно на 30 минут раньше пешехода, при этом его скорость была в 5 раз больше скорости велосипедиста. Сколько времени затратил велосипедист на путь от Скиделя до Гродно? В ответ запишите только число, выражающее время в минутах.
4. У Юры на дне рождения было пятеро друзей. Первому он отрезал часть торта, второму часть остатка, третьему часть того, что осталось, четвертому часть нового остатка. Последний кусок Юра разделил пополам с пятым другом.Кому из друзей достался самый большой кусок?
5. Скорость движения Земли вокруг Солнца 29,8 км/с, а скорость движения Марса на 5,7 км/с меньше.Найдите, какой путь пройдет Марс за 16,8 с.
6. Найдите значение выражения 2,08(8,2+3,75-12,016 .
7. Найдите угол между часовой и минутной стрелкой в 14 часов 30 минут.
8. Когда оловянные солдатики строились в колонну по 4, по 5 или по 6 человек, то каждый раз один оставался лишним, а когда построились в колонну по 7, то лишних не осталось. Какое могло быть наименьшее количество оловянных солдатиков?
9. В ящике лежат 2014 черных и 2014 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было 2 шара белого цвета?
10. Найдите наименьшее общее кратное чисел 168, 231 и 60.
11. Дробь равна целому числу, причем разным буквам соответствуют разные цифры, а между ними стоит знак умножения. Найдите, чему равна эта дробь.
12. На какую степень числа 3 делится произведение натуральных чисел от 1 до 100 включительно?
Задачи олимпиады "Третье тысячелетие" для 6 класса
1. Назовём «тяжёлым» месяц, в котором пять понедельников. Сколько тяжёлых месяцев может быть в течение года?
2. Андрей перемножил две последовательные цифры и получил в итоге двузначное число, записываемое двумя последовательными цифрами. Найдите все такие примеры.
3. Саша зачеркнул на 25-й странице учебника все слова, в которых нет буквы А, потом он зачеркнул все слова, в которых нет буквы Б, а потом он нашел все слова, где есть и буква О, и буква А, и тоже зачеркнул их. Костя на той же странице своего учебника зачеркнул слова, где нет Б, но есть А или О (возможно, обе сразу), и после этого он зачеркнул все слова, где нет ни буквы А, ни буквы О. Могло ли у Саши остаться незачеркнутыми больше слов, чем у Кости?
4. В каждом из двух классов по 30 учеников. Мальчиков в первом классе в 2 раза больше, чем во втором, а девочек – в 3 раза меньше. Сколько мальчиков и девочек в каждом классе?
5. Три ручки, четыре карандаша и линейка вместе стоят 26 рублей, а пять ручек, шесть карандашей и три линейки - 44 рубля. Сколько стоят вместе две ручки и три карандаша?
6. Первоначально на доске написано число 1. Разрешается любое написанное на доске число умножить на 2 или переставить в нём цифры. Можно ли таким образом получить 209?
Олимпиада - Формула Единства
- www.formulo.org/ru/olimpiada
«А давайте посчитаем, благородные кроты»
Г. Х. Андерсен, «Дюймовочка»
Математике должно учить в школе еще с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни. Н.И. Лобачевский
Математика 6 класс. Правила. Задания. Решения
Решебник по математике для 6 класса авторы Кузнецова Муравьева Шнеперман
Ответы к рабочей тетради по математике 6 класс авторов Кузнецова, Муравьёва, Шнеперман
Сборник задач по математике. 6 класс для общеобразовательных учреждений с русским языком обучения авторов Кузнецовой Е.П., Муравьевой Г.Л., Шнепермана Л.Б.
Математика(готовые домашние задания) 6 класс.Математика. Учебное пособие для 6 класса общеобразовательных учреждений с русским языком обучения, под редакциейЛ.Б. Шнипермана, авторы Е.П. Кузнецова, Г.Л. Муравьева, Л.Б. Шниперман, Б.Ю. Ящин, Ю.К. Войтова
Упражнения для устного счета
Тексты работ составлены с учетом наиболее типичных ошибок, допускаемых учащимися при вычислениях
Работа № 1.
1-15.Вычислите устно и запишите только ответы.
1. 48·7/8 6. 64·1/8 11. 90·1/3
2. 48·5/12 7. 64·3/8 12. 90·2/3
3. 48·3/4 8. 64·3/4 13. 90·1/6
4. 48·3/16 9.64·1/16 14. 90·5/6
5. 48·5/6 10. 64·5/16 15. 90·5/18
Работа № 2.
1-15.Вычислите устно и запишите только ответы.
1. 5·3/20 6. 8·7/16 11. 9·5/18
2. 3·4/15 7. 8·9/32 12. 12·11/36
3. 5·8/25 8. 20·11/40 13. 36·11/72
4. 10·13/40 9.5·4/15 14. 4·15/16
5. 18·17/36 10. 6·7/12 15. 14·17/28
Работа №3.
1-15.Вычислите устно и запишите только ответы.
1. 60·1/2 6. 60·2/3 11. 60·1/8
2. 60·1/3 7. 60·3/4 12. 60·3/8
3. 60·1/4 8. 60·2/5 13. 60·5/8
4. 60·1/5 9.60·3/5 14. 60·7/8
5. 60·1/6 10. 60·5/6 15. 60·(1 и 1/8)
Работа № 4.
1-15.Вычислите устно и запишите только ответы.
1. 8·5/12 6. 6·9/20 11. 15·11/24
2. 4·7/20 7. 6·5/27 12. 40·1/6
3. 12·5/18 8. 15·1/20 13. 75·1/10
4. 12·3/16 9.15·1/25 14. 20·7/12
5. 16·7/18 10. 15·1/20 15. 18·4/27
Отрывок из статьи А. Шевкина "Текстовые задачи в школьном курсе математики. (5-9 классы)": |
Шестому классу дано задание решить с помощью уравнения известную задачу из «Арифметики» Л.Ф. Магницкого: "Некий человек нанял работника на год, обещал ему дать 12 руб. и кафтан. Но тот, отработав 7 месяцев, захотел уйти и просил достойной платы с кафтаном. Хозяин дал ему по достоинству расчет 5 р. и кафтан. Спрашивается, а какой цены тот кафтан был?" |
Алгебраическое решение задачи приводит к уравнению 7 · (x + 12):12 = x + 5, где x руб. — стоимость кафтана. Ученица 6 класса Аня А. предложила вычислять стоимость одного месяца проще: работник не получил 12 – 5 = 7 (руб.) за 12 – 7 = 5 (месяцев), поэтому за один месяц ему платили 7:5 = 1,4 (руб.), а за 7 месяцев он получил 7 ·1,4 = 9,8 (руб.), тогда кафтан стоил 9,8 – 5 = 4,8 (руб.). ...Возьмем старинную китайскую задачу: "В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Конечно, следуя «правилам оптимальной стратегии», можно составить уравнение:Узнать число фазанов и число кроликов." 4x + 2 · (35 – x) = 94, где x — число кроликов, и получить ответ задачи. ... Диалог, найденный нами у старых мастеров методики математики и вызывающий у детей живейшее участие в решении задачи (в скобках показаны действия, выполняемые для получения ответа на вопрос): — Дети, представим, что на верх клетки, в которой сидят фазаны и кролики, мы положили морковку. Все кролики встанут на задние лапки, чтобы дотянуться до морковки. Сколько ног в этот момент будет стоять на земле? — 70 (35·2 = 70). — Но в условии задачи даны 94 ноги, где же остальные? — Остальные не посчитаны — это передние лапы кроликов. — Сколько их? — 24 (94 – 70 = 24). — Сколько же кроликов? — 12 (24:2 = 12). — А фазанов? — 23 (35 – 12 = 23). Приведем последний пример, показывающий возможности арифметических способов решения задач. На этот раз рассмотрим упрощенный вариант старинных китайских задач и задач из «Всеобщей арифметики» И. Ньютона: "Мама раздала детям по четыре конфеты, и три конфеты остались лишними. А чтобы дать детям по пять конфет, двух конфет не хватает. Сколько было детей? " ...Диалог:— Представим, что мама раздала детям по четыре конфеты. Сколько конфет у нее осталось? — Три. — Если она продолжит раздавать конфеты, то по сколько конфет она даст каждому? — По одной (5 – 4 = 1). — Скольким детям хватит еще по одной конфете? — Троим. — А скольким не хватит? — Двоим. — Сколько же было детей? — Пять (3 + 2 = 5). |
| Вся статья А. Шевкина: Текстовые задачи в школьном курсе математики. (5-9 классы)" |
Шуточный тест.
Отвечайте вслух, и только потом проверяйте свой ответ.
1. Вопрос: Что вы кладете в тостер?
Ответ. ХЛЕБ. Если вы кладете что-то другое, будьте осторожны! Если вы сказали "хлеб", переходите ко 2му вопросу.
2. Вопрос. Скажите слово "далеко" 5 раз. Назовите его по буквам: д-а-л-е-к-о. Что пьют коровы?
Ответ: Коровы пьют воду. Если Вы сказали "молоко", пожалуйста не делайте попытку ответить на следующий вопрос. Ваш мозг, очевидно, переутомлен и может даже перегреться. Может быть, вам следует отдохнуть и почитать журнал "Весёлые картинки". Если вы сказали "воду", переходите к следующему вопросу.
3. Вопрос. Двадцать лет назад самолет летел на высоте 10 км над Германией. Если вы помните, 20 лет назад Германия была политически разделена на две части - Западную и Восточную. И вот, во время полета два двигателя отказали. Пилот, чувствуя, что последний двигатель тоже вот-вот заглохнет, решается на аварийную посадку. К сожалению, двигатель заглох раньше, и самолет упал на нейтральной территории между Западной Германией и Восточной. Где бы вы похоронили оставшихся в живых? В Западной Германии или в Восточной или на нейтральной территории?
Ответ. Конечно, не надо хоронить оставшихся в живых! Если вы сказали что-то другое, вы - настоящий остолоп, и вы никогда не должны участвовать в спасательных работах после авиакатастрофы. Если вы ответили: "не хоронят оставшихся в живых", тогда переходите к следующему вопросу.
4. Вопрос. Если стрелка передвигается на 1/60 градуса каждую минуту, на сколько градусов она переместится за час?
Ответ: На один градус. Если вы сказали "360 градусов", или что-то ещё, отличное от ответа "Один градус", вам тут не место. Выключите компьютер и идите займитесь чем-нибудь другим.
:)
Задачи которые может решить каждый.
Математический кружок. 6-7 классы
Лист самоконтроля 7 (6 класс)
1.Как вводятся координаты на плоскости?(Вопрос 1 на ст.228)
2.У точек какой прямой координатной плоскости одинаковые: а) абсциссы; б) ординаты?(Вопрос 3 на ст.228)
3.Как найти координаты точки координатной плоскости? (Вопрос 5 на ст.228)
4.Что такое координатные углы (четверти)? Сколько их? (Вопрос 7 на ст.228)
5.Как построить по формуле график: а) прямой пропорциональности; б) обратной пропорциональности (Вопрос 2 на ст.235)
6.Запишите формулу линейной зависимости. (Вопрос 1 на ст.239)
7.Сформулируйте правило умножения: а) двух чисел разных знаков; б) двух отрицательных чисел (Вопрос 1 на ст.245)
8.Какие числа называются взаимно обратными? (Вопрос 1 на ст.254)
9.Как разделить два числа с разными (одинаковыми) знаками?(Вопрос 2 на ст.259)
10.Как найти: а) длину окружности; б) площадь круга?(Вопрос 2 на ст.263)
11.Что значит возвести число а в n-ю степень? (Вопрос 3 на ст.275)
12.Как степени с натуральными показателями: а) умножают; б) делят? (Вопрос 1 на ст.278)
13.Как возводят в степень произведение?(Вопрос 2 на ст.283)
14.Чему равна степень ас целым отрицательным показателем –n?(Вопрос 3 на ст.288)
15.Что называется биссектрисой?(Вопрос 2 на ст.25)
Лист самоконтроля 8 (6 класс)
1.Как называется первая (вторая) координата точки координатной плоскости? (Вопрос 2 на ст.228)
2.Какой вид имеют координаты точек: а) оси абсцисс; б) оси ординат; в) начала координат? (Вопрос 4 на ст.228)
3.Как построить точку по ее координатам? (Вопрос 6 на ст.228)
4.Запишите формулу: а) прямой пропорциональности; б) обратной пропорциональности. (Вопрос 1 на ст.235)
5.Как построить график линейной зависимости?(Вопрос 2 на ст.239)
6.Сформулируйте распределительный закон умножения относительно сложения.(Вопрос 2 на ст.251)
7.Как раскрываются скобки, когда перед ними стоит знак: а) «+»; б) «-»? (Вопрос 4 на ст.251)
8.Как разделить одно число на другое?(Вопрос 1 на ст.259)
9.Чему равно отношение длины окружности к длине ее диаметра? (Вопрос 1 на ст.263)
10.Как в выражении аn называются числа аи n?(Вопрос 2 на ст.275)
11.Положительное или отрицательное число получится при возведении отрицательного числа в степень: а) четную; б) нечетную?(Вопрос 5 на ст.275)
12.Как возводят степень в степень?(Вопрос 1 на ст.283)
13.Как возводят в степень дробь (частное)? (Вопрос 3 на ст.283)
14.Как называется запись u=a·10k? Какими могут быть числа: u, а,k?(Вопрос 1 на ст.292)
15.Какой треугольник называется равнобедренным?(Вопрос 2 на ст.52)
Инструкция по решению задачи на разрезание фигуры
Электронная физико-техническая школа (стоимость участия)
еФТШ Карта сокровищ 2014(получить условие, отправить решение)
Карта сокровищ.Всероссийский математический конкурс
«Квант» для «младших» школьников
Математические олимпиады по лигам
Головоломки для умников и умниц
Лист самоконтроля 5 (6 класс)
1.Что называется отношением двух: а) чисел; б) величин?(Вопрос 1 на ст.122)
2.Сформулируйте: а) основное свойство пропорции; б) признак пропорции.(Вопрос 4 на ст.129)
3.Какие величины называются прямо пропорциональными?(Вопрос 1 на ст.132)
4. Что значит разделить число m пропорционально числам p и q?(Вопрос 1 на ст.140)
5. Что называется масштабом карты (чертежа, плана)? Что означает масштаб чертежа: а) 1:5; б) 10:1?(Вопрос 1,2 на ст.146)
6.Что называется процентом?(Вопрос 1 на ст.152)
7. Как выразить десятичную дробь в виде процентов?(Вопрос 3 на ст.152)
8.Как найти число по его процентам?(Вопрос 1 на ст.158)
9.Укажите фигуры, имеющие: а) одну ось симметрии; б) две оси симметрии.(Вопрос 1 на ст.175)
10.Какие числа называются рациональными?(Вопрос 3 на ст.179)
11.Как построить точку К1, симметричную точке К относительно точки О?(Вопрос 2 на ст.190)
12.Какие два числа называются противоположными друг другу?(Вопрос 1 на ст.194)
13.Что называется модулем: а) положительного числа; б) отрицательного числа; в) нуля?(Вопрос 1 на ст.199)
14.Сфомулируйте правило сравнения двух чисел.(Вопрос 1 на ст.203)
15.Как сложить два отрицательных числа?(Вопрос 1 на ст.210)
16.Как из одного числа вычесть другое?(Вопрос 1 на ст.218)
Лист самоконтроля 6 (6 класс)
1.Как найти во сколько раз одно число больше другого; б) какую часть одно число составляет от другого?(Вопрос 3 на ст.122)
2.Что называется пропорцией? Как называются в пропорции а:b=c:dчисла: а) а и d; в) b и с?(Вопрос 1,3 на ст.128)
3.Как найти неизвестный средний (крайний) член пропорции?(Вопрос 5 на ст.129)
4.Какие величины называются обратно пропорциональными?(Вопрос 1 на ст.136)
5.Как разделить число m: а) в отношении p:q; б) пропорционально числам p,q,t?(Вопрос 2 на ст.140)
6.Как выразить 17% в виде дроби: а) десятичной; б) обыкновенной?(Вопрос 2 на ст.152)
7.Как найти несколько процентов данного числа?(Вопрос 4 на ст.152)
8.Кавк найти: а) сколько процентов одно число составляет от другого; б) процентное отношение двух чисел?(Вопрос 2 на ст.158)
9.Расскажите, как построить точку, симметричную данной относительно некоторой прямой.(Вопрос 2 на ст.175)
10.Какую прямую называют координатной прямой?(Вопрос 1 на ст.184)
11.Приведите примеры центрально-симметричных фигур.(Вопрос 1 на ст.190)
12.Какой знак имеет число, противоположное положительному числу? Отрицательному числу?(Вопрос 3 на ст.194)
13.Чему равен модуль числа?(Вопрос 2 на ст.195)
14.Как сравнить два отрицательных числа?(Вопрос 4 на ст.203)
15.Как сложить два числа с разными знаками и разными модулями?(Вопрос 2 на ст.210)
16.Как найти расстояние между двумя точками координатной прямой?(Вопрос 1 на ст.222)
Перевод чисел из одной системы счисления в другую онлайн
Учимся решать логические задачи
Онлайн калькуляторы для решения задач по математике
Тесты по математике онлайн в Online Test Pad
Интернет-Олимпиада по математике "Сократ" - для школьников 1-10 классов - сейчас!
Регистрация участников олимпиады "Сократ"
Математический праздник. Разбор задач 6 класса
23-25.01.2014 года. 2-й этап дистанционной олимпиады по математике Гродненского университета.
6 класс
1.Леша задумал число. Если его увеличить в 2 раза, а потом результат уменьшить на 12,86, то получится 27,14. Какое число задумал Леша?
2. Решите уравнение 35: х = 9,1:5,2
Ответ 1 0,05
Ответ 2 61,25
Ответ 3 20
Ответ 4 165620
3. Определите, сколько четырехзначных чисел вида 5*1* делятся на 6. В ответ запишите только количество чисел.
Решение.
На 6 делятся те и только те числа, которые делятся на 2 и на 3 одновременно. На два делятся те и только те числа, которые оканчиваются цифрами 0, 2, 4, 6, 8.
1)Среди чисел 5*10 делятся на 3 четыре числа: 5010, 5310Ю 5610 и 5910.
2) Среди чисел 5*12 делятся на 3 три числа: 5112, 5412, 5712.
3)Среди чисел 5*14 делятся на 3 три числа: 5214, 5514, 5814.
4)Среди чисел 5*16 делятся на 3 четыре числа: 5016, 5316, 5616, 5916.
5)Среди чисел 5*18 делятся на 3 три числа: 5118, 5418, 5718
Следовательно, на 6 делятся 17 чисел.
Ответ: 17.
4. В ящике лежат 2012 черных и 2013 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было 2 шара белого цвета?
Ответ: 2014.
5. Число 87 составляет 29% от данного числа. Найдите среднее арифметическое этих чисел.
Ответ: 193,5.
6. Когда оловянные солдатики строились в колонну по 4, по 5 или по 6 человек, то каждый раз один оставался лишним, а когда построились в колонну по 7, то лишних не осталось. Какое могло быть наименьшее количество оловянных солдатиков?
Ответ 1 121
Ответ 2 181
Ответ 3 301
Ответ 4 308
Ответ 5 241
Решение.
Из данных чисел на 7 делятся 301 и 308. Но 308 делится на 4. Следовательно, искомое число – 301.
Ответ: 301.
7. На какую степень числа 7 делится произведение натуральных чисел от 1 до 2014 включительно?
Решение.
Чтобы найти максимальную степень 7, на которое делится все произведение, нужно найти, сколько всего раз 7 встречалась в качестве простого множителя каждого из перемноженных чисел. 2014/7=287 (ост. 5), то есть среди перемноженных чисел (в их числе будут 7*1, 7*2, 7*3.. 7*287) семерка встречается 287 раз и дважды в 49, и трижды в 343, т. е. еще 1+2 = 3 раза. Таким образом, данное произведение делится на 290-ю степень числа 7
Ответ: 290.
8. Проволоку длиной 34 и ½ метра разрезали на три части. Первая часть составила 1/4 всей проволоки, вторая – 8/9 проволоки, оставшейся после того, как отрезали первую часть. Какова длина в метрах второй части?
Ответ 1 32
Ответ 2 25
Ответ 3 23
Ответ 4 8
Решение.
(¼)·(69/2) = 69/8(м) – первая часть.
69/2 – 69/8 = 207/8 (м) – осталось.
(8/9)·(207/8) = 23 (м) – длина второй части.
Ответ: 23.
9. Найдите угол (в градусах) между часовой и минутной стрелкой в 20 часов 14 минут
Решение
1)360°:12=30° -- проходит часовая стрелка за 1 ч.
30°·8=240° -- пойдет часовая стрелка за 8 часов.
(30°·14)/60= 7° - пройдет часовая стрелка за 14 мин.
240°+7°=247° -- пройдет часовая стрелка за 8 ч 14 мин.
2)360°:60 = 6° -- проходит минутная стрелка зам 1 мин.
6°·14 = 84° -- пройдет минутная стрелка за 14 мин.
3) 247° - 84° = 163°.
Ответ: 163°.
10. Расстояние между велосипедистом и пешеходом равно 26,1 км. Скорость пешехода 5,8 км/ч, а скорость велосипедиста в 2,5 раза больше. За какое время (в минутах) велосипедист догонит пешехода, если они оба двигаются по одной дороге в одном направлении?
Решение.
5,8·2,5 = 14,5 (км/ч) – скорость велосипедиста.
14,5 – 5,8 = 8,7 (км/ч) – скорость сближения велосипедиста и пешехода.
26,1: 8,7 = 3(ч) = 180 (мин).
Ответ: 180 мин.
11. К некоторому трехзначному числу приписали цифру 7 сначала слева, а затем справа и от первого четырехзначного числа отняли второе и получили 873. Найдите исходное число.
Решение.
Пусть искомое трехзначное число имеет вид QUOTE 12abc"> 12abc"> . После приписывания к нему слева и справа цифры 7 получим четырехзначные числа QUOTE 127abc Рё abc7"> 127abc Рё abc7"> . Имеем разность. Откуда, c= 0, b= 8, a= 6. Исходное число равно 680.
Ответ: 680.
12.За 16 жевательных резинок Джон заплатил столько долларов, сколько жевательных резинок можно купить на доллар. Сколько центов стоит одна жевательная резинка?
Решение.
16 резинок – х $
х резинок – 1 $
Отсюда х2 = 16, х = 4, т. е. 4 резинки стоят 1$ =100 центов, а одна – 25 центов.
Ответ: 25 центов.
Лист самоконтроля 3 (6 класс)
1.Как умножить десятичную дробь: а) на 0,1; б) на 0,01; в) на 0,001?
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001, надо в этой дроби перенести запятую соответственно на один, два, три знака влево.
2.Как перемножить две десятичные дроби?
Чтобы перемножить две десятичные дроби, их надо перемножить как натуральные числа (т. е. не обращая внимание на запятые), а в полученном произведении отделить запятой справа столько десятичных знаков, сколько их в обоих множителях вместе.
3.Как поступают, если при умножении десятичных дробей произведение соответствующих натуральных чисел:
а) оканчивается одним или несколькими нулями;
б) содержит меньше знаков, чем надо отделить запятой?
Если при умножении десятичных дробей произведение натуральных чисел оканчивается одним или несколькими нулями, то сначала в этом произведении отделяют с помощью запятой необходимое количество десятичных знаков, а лишь затем отбрасывают нули.
Если при умножении десятичных дробей в произведении натуральных чисел получается меньше знаков, чем надо отделить запятой, то перед полученным произведением дописывают необходимое количество нулей.
4.Сфомулируйте: а) переместительный закон умножения; б) сочетательный закон умножения; в) распределительный закон умножения относительно сложения.
а) Для любых чисел а и b верно равенство а·b=b·а.
б) Для любых чисел а,b и с верно равенство (а·b)·c=a·(b·c).
в) Для любых чисел а,b и с верно равенство (а+b)·c=a·c+b·c.
5.Как найти 0,85 числа?
Надо число умножить на 0,85.
6.Что больше: а) 0,73 от 0,037 или 0,037 от 0,73; б) 0,73 числа 3,7 или 0,37 числа 7,3?
а) 0,037· 0,73 = 0,73· 0,037;
б) 3,7· 0,73 = 7,3·0,37.
7. Как обратить десятичную дробь в обыкновенную?
Чтобы обратить десятичную дробь в обыкновенную, можно:
1) записать целую часть дроби, а если это 0, то вообще ее не писать;
2) в числителе дробной части записать число, стоящее после запятой, а в знаменателе записать единицу и столько нулей, сколько знаков справа от запятой.
8.Назовите действия первой и второй ступени.
Сложение и вычитание называют действиями первой ступени. Умножение и деление называют действиями второй ступени.
9. В каком порядке выполняются действия в числовом выражении: а) без скобок; б) со скобками?
1. Если в выражении нет скобок и оно содержит действия только одной ступени, то эти действия выполняют по порядку слева направо.
2. Если в выражении нет скобок и оно содержит действия разных ступеней, то сначала выполняют умножение и деление (слева направо), а затем сложение и вычитание (слева направо).
3.Если в выражении есть скобки, то сначала выполняют все действия в скобках (слева направо), а затем все действия в полученном выражении (слева направо).
10.Как найти число а, зная, что 0,45 этого числа равны 1,8?
а= 1,8:0,45.
11.Составьте задачу на нахождение числа по его части.
На отделку платья пошло 0,3 м шелка, что составляет 0,12 всей ткани, необходимой на его пошив. Сколько метров ткани пошло на пошив платья?
12.Какие из сторон равнобедренного треугольника называют: а) боковыми; б) основанием?
Две равные стороны равнобедренного треугольника называются боковыми сторонами, а третья сторона – основанием.
13. Сформулируйте свойство углов треугольника: а) равнобедренного; б) равностороннего.
В равнобедренном треугольнике углы при основании равны.
В равностороннем треугольнике все углы равны.
14.Что можно сказать о треугольнике: а) с двумя равными углами; б) с тремя равными углами?
Если два угла треугольника равны, то треугольник равнобедренный.
Если три угла треугольника равны, то треугольник равносторонний.
15. Как сравнить две десятичные дроби?
Из двух десятичных дробей меньше та, у которой целая часть меньше.
Если целые части десятичных дробей равны, то та из них меньше, у которой число десятых меньше.
Если целые части десятичных дробей равны и числа десятых равны, то та из них меньше, у которой число сотых меньше и т. д.
Из двух чисел меньше то, которому на горизонтальном координатном луче соответствует точка, расположенная левее.
Лист самоконтроля 4 (6 класс)
1.Как разделить десятичную дробь: а) на 10; б) на 100; в) на 1 000 000?
Чтобы разделить десятичную дробь на 10, 100, 1 000 000 нужно в этой дроби перенести запятую соответственно на один, два, шесть знаков влево.
2. Как разделить десятичную дробь: а) на 0,1; б) на 0,01; в) на 0,00001?
Чтобы разделить десятичную дробь на 0,1; 0,001; 0,00001 нужно в этой дроби перенести запятую соответственно на один, три, пять знаков вправо.
3.Как изменится десятичная дробь, если в ней перенести запятую влево на 1, на 3, на 5 знаков?
Десятичная дробь уменьшится в 10, 1000 и 100 000 раз соответственно.
4.Как разделить десятичную дробь на натуральное число?
Чтобы разделить десятичную дробь на натуральное число, нужно разделить ее на это натуральное число уголком по правилу деления натуральных чисел – при этом запятую в частном поставить, как только закончится деление целой части дроби.
5.На каком свойстве основано правило деления десятичных дробей?
Если делимое и делитель умножить на одно и то же число, не равное нулю, то частное не изменится.
6. Как разделить десятичную дробь на десятичную дробь?
Чтобы разделить десятичную дробь на десятичную дробь, можно в делимом и делителе перенести запятую на столько знаков вправо, сколько их после запятой в делителе, а затем выполнить деление на натуральное число.
7.Какую обыкновенную дробь можно обратить в десятичную?
Обратить в десятичную можно только такую обыкновенную дробь, знаменатель которой после сокращения не имеет никаких простых множителей, кроме 2 и 5.
8.Как обыкновенную дробь обратить в десятичную?
Тремя способами:
1.В ряду чисел 10; 100; 1000 и т. д. подобрать такое, которое делится на знаменатель обыкновенной дроби, и привести ее к этому знаменателю.
2.Знаменатель обыкновенной дроби разложить на простые множители и уравнять в нем количество двоек и пятерок.
3.Разделить числитель дроби на знаменатель по правилу деления десятичных дробей.
9. Как можно находить значение выражения с десятичными и обыкновенными дробями?
При выполнении примеров на действия с десятичными и обыкновенными дробями всегда можно все дроби записать в виде обыкновенных дробей. Некоторые обыкновенные дроби можно выразить конечной десятичной дробью.
10.Всегда ли значение выражения находят «по действиям»?
Выполнять вычисления можно и «цепочкой».
11.Какие углы называются равными?
Два угла называются равными, если один из них можно наложить на другой так, что они совместятся.
12.Что называется биссектрисой угла?
Биссектрисой угла называется луч с началом в его вершине, который делит угол на два равных угла.
13.Чем может определяться вид треугольника?
Вид треугольника может определяться величиной его углов или числом его равных сторон.
14.Какой треугольник называется: а) остроугольным; б) прямоугольным; в) тупоугольным; г) равнобедренным; д) равносторонним; е) разносторонним?
Если все углы треугольника острые, то он называется остроугольным. Если один из углов треугольника прямой, то он называется прямоугольным. Если один из углов треугольника тупой, то он называется тупоугольным. Если две стороны треугольника равны, то он называется равнобедренным. Если все стороны треугольника равны, то он называется равносторонним. Если все стороны треугольника имеют разные длины, то он называется разносторонним.
15.Как округлить число до десятых? До тысячных? До целых?
Чтобы округлить число до десятых, тысячных, целых можно:
1) все следующие за этим разрядом цифры отбросить;
2) если первая отброшенная цифра 5, 6, 7, 8, 9, то полученное число увеличить на единицу разряда, до которого округляем;
3) если первая отброшенная цифра 0, 1, 2, 3, 4, то полученное число оставить без изменения.
Лист самоконтроля 3
1.Как умножить десятичную дробь: а) на 0,1; б) на 0,01; в) на 0,001?
2.Как перемножить две десятичные дроби?
3.Как поступают, если при умножении десятичных дробей произведение соответствующих натуральных чисел:
а) оканчивается одним или несколькими нулями;
б) содержит меньше знаков, чем надо отделить запятой?
4.Сфомулируйте: а) переместительный закон умножения; б) сочетательный закон умножения; в) распределительный закон умножения относительно сложения.
5.Как найти 0,85 числа?
6.Что больше: а) 0,73 от 0,037 или 0,037 от 0,73; б) 0,73 числа 3,7 или 0,37 числа 7,3?
7. Как обратить десятичную дробь в обыкновенную?
8.Назовите действия первой и второй ступени.
9. В каком порядке выполняются действия в числовом выражении: а) без скобок; б) со скобками?
10.Как найти число а, зная, что 0,45 этого числа равны 1,8?
11.Составьте задачу на нахождение числа по его части.
12.Какие из сторон равнобедренного треугольника называют: а) боковыми; б) основанием?
13. Сформулируйте свойство углов треугольника: а) равнобедренного; б) равностороннего.
14.Что можно сказать о треугольнике: а) с двумя равными углами; б) с тремя равными углами?
15. Как сравнить две десятичные дроби?
Лист самоконтроля 4
1.Как разделить десятичную дробь: а) на 10; б) на 100; в) на 1 000 000?
2. Как разделить десятичную дробь: а) на 0,1; б) на 0,01; в) на 0,00001?
3.Как изменится десятичная дробь, если в ней перенести запятую влево на 1, на 3, на 5 знаков?
4.Как разделить десятичную дробь на натуральное число?
5.На каком свойстве основано правило деления десятичных дробей?
6. Как разделить десятичную дробь на десятичную дробь?
7.Какую обыкновенную дробь можно обратить в десятичную?
8.Как обыкновенную дробь обратить в десятичную?
9.Как можно находить значение выражения с десятичными и обыкновенными дробями?
10.Всегда ли значение выражения находят «по действиям»?
11.Какие углы называются равными?
12.Что называется биссектрисой угла?
13.Чем может определяться вид треугольника?
14.Какой треугольник называется: а) остроугольным; б) прямоугольным; в) тупоугольным; г) равнобедренным; д) равносторонним; е) разносторонним?
15.Как округлить число до десятых? До тысячных? До целых?
Результаты белорусских участников конкурса "Кенгуру" 2003-2013
Бесплатный IQ тест онлайн (30 минут, 40 вопросов)
Онлайн калькуляторы для решения задач по математике
Математика, 6 класс (Е. П. Кузнецова и др.) 2010
Развивающие игры и тренажёры по математике
Упражнение на скорость мышления «Быстроглаз»
Упражнения «Математик» и «Капли»
Дистанционная олимпиада продолжается.
Друзья! Решите предлагаемые ниже задачи и пришлите полученные вами результаты и рассуждения по обратной связи (смотрите в меню сайта «Контакты»). Фамилии участников и набранное ими количество баллов за решение задач будут опубликованы на сайте.
Задания недели 05.10.2013 – 12.10.2013:
16. Плоскость окрашена в два цвета. Докажите, что найдутся две точки, отстоящие друг от друга на расстоянии 1 м, окрашенные одинаково.
17. В ящике 100 черных и 100 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было 2 шара белого цвета?
18. Три подруги одеты в белое, зеленое и синее платья. Их туфли также белого, зеленого и синего цветов. Известно, что у Ани цвет платья и туфель совпадали. Ни платье, ни туфли Вали не были белыми. Наташа – в зеленых туфлях. Определите цвет платьев и туфель каждой из подруг.
19. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом находится между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Как распределены эти жидкости по сосудам?
20. Разрежьте фигуру на четыре равные части и сложите из этих частей квадрат с квадратным отверстием посередине:
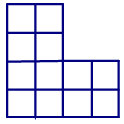 Всем желаем успехов в решении заданий 16-20 нашей олимпиады! Не сдаваться! Ждем ваших сообщений.
Всем желаем успехов в решении заданий 16-20 нашей олимпиады! Не сдаваться! Ждем ваших сообщений.
www.edu.grsu.by/math Гродненская обл. дист. олимп. по мат. для 5 -7 кл.
6 класс (23-26.10.2013)
1.Числа 90 и 100 разделили на одно и тоже число. В первом случае получили остаток 18, а во втором случае – остаток 4. Найдите делитель.
Ответ: 24
2. Вычислите: 75 + 76 + 77 + …+2013.
Ответ: 2024316
3. Найдите сумму всех делителей числа 120.
Ответ: 360
4. Уменьшаемое увеличили на 10,8, а вычитаемое уменьшили на 12,5. В результате разность стала равной 45,3. На сколько вычитаемое было меньше уменьшаемого?
Ответ:22
5. Сторона квадрата равна 0,4 дм. Найдите сторону квадрата в дециметрах, площадь которого составляет 0,25 площади данного квадрата.
В ответ запишите только число.
Ответ: 0,2
6. Расстояние между двумя причалами 35 км. Сколько времени в минутах потратит теплоход на путь по реке от одного причала до другого и обратно, если собственная скорость теплохода 17 км/ч, а скорость течения реки 3 км/ч?
В ответ запишите только число.
Ответ: 255
7. Толя поспорил с Сашей, что сможет угадать, какого числа тот родился. Толя попросил Сашу умножить число своего рождения на 7, разделить на 3, умножить на 4, разделить на 5, умножить на 11 и разделить на 8. После этого он спросил у Саши, целое ли получилось число. Когда Саша ответил, что целое, Толя сказал, что уже может угадать число его рождения. Так какого же числа родился Саша?
Ответ: 30
8. Определите количество нулей, которыми заканчивается произведение первых 2013 натуральных чисел.
Ответ: 501
9. Вычислите: 0,5(20,12·20,13 – 6,039·0,4)·10.
Ответ: 2013
10. У Олега спросили, сколько человек учится в его классе, на что тот ответил: " Ровно у половины из них любимый предмет - математика. 0,25 класса предпочитает математике литературу. Еще 1/5 ничем, кроме физкультуры, не интересуется. Ну и еще есть Вовочка, которому вообще ничего не интересно". Сколько же человек в классе?
Ответ: 20
11. В равнобедренном треугольнике сумма длин боковых сторон равна 1118 см, а длина основания на 336 см больше длины боковой стороны. Найдите периметр треугольника в сантиметрах. Ответ запишите только число.
Ответ: 2013
12. Решите уравнение
(х + 71,2) – 37,6 = 95,61.
Ответ: 62,01
Контрольная работа 2
к главе 2 «Сложение и вычитание десятичных дробей»
Вариант 1.
1.Укажите, в каком случае правильно выполнено вычитание дробей:
а) 10,64 – 3,3351 = 7, 349; б) 10,64 – 3,3351 = 7, 3049;
в) 10,64 – 3,3351 = 7, 3149; г) 10,64 – 3,3351 = 7, 3059.
Ответ: б) 10,64 – 3,3351 = 7, 3049.
2.Найдите значение выражения и результат округлите до сотых:
1) 0,273 + 2,316; 2) 0,58 + 0,2539;
2) 5,0074 + 12, 679; 4) 4,5837 – 3,2637;
5) 1,011 – 0,444; 6) 1 – 0,076.
Ответ: 1) 0,273 + 2,316 = 2,589; 2) 0,58 + 0,2539 = 0,8339;
2) 5,0074 + 12, 679 = 17,6864; 4) 4,5837 – 3,2637 = 1,32;
5) 1,011 – 0,444 = 0,567; 6) 1 – 0,076 = 0,924 .
3.Найдите значение выражения:
1) 0,7 + 0,15 + 0,3; 2) 6,072 + 4,9 + 2,028;
3) 0,954 + 0,63 + 0,046 + 1,47.
Ответ: 1) 0,7 + 0,15 + 0,3 = 1,15; 2) 6,072 + 4,9 + 2,028 = 13;
3) 0,954 + 0,63 + 0,046 + 1,47 = 3.
4. Найдите значение выражения:
1) 8 – 7,9 + 7,8 – 7,7 + 7,6 – 7,5;
2) 50,48 + (168,3 – 15,48) ;
3) 8,7 + (100 – (12,91 – 11,97)) .
Ответ: 1) 8 – 7,9 + 7,8 – 7,7 + 7,6 – 7,5 = 0,3;
2) 50,48 + (168,3 – 15,48) = 213,3;
3) 8,7 + (100 – (12,91 – 11,97)) = 108,7 – 0,94 = 107,76.
5.Найдите сумму и разность:
1) 24,326 кг и 12 кг 657 г; 2)12 м 692 мм и 9,308 м.
Ответ: 1) 24,326 кг + 12, 657 кг = 36, 983 к г;
24,326 кг – 12, 657 к г = 11,669 кг.
2) 12, 692 м + 9,308 м = 22 м;
12, 692 м – 9,308 м = 3,384 м.
6.Запишите три приближенных значения числа 8,42306:
1) с недостатком; 2) с избытком.
Ответ:1) 8,4; 8,42; 8,423.
2) 8,4231; 8,4232; 8,4233.
7.Решите уравнение:
1) х – 13,4 = 9,17; 2)96,18 – х = 20,5;
3) (х– 93,4) – 15,4 = 106,72;
4) 118 + (х– 102,6) = 142,2.
Ответ:1) 22,57; 2) 75,68; 3) 215, 52; 4) 126,8.
8.Скорость течения реки 3,8км/ч. Собственная скорость катера 18,5 км/ч. Найдите скорость катера по течению и против течения.
Ответ:по течению 3,8 + 18,5 = 22,3 км/ч, против течения 18,5 – 3,8 = 14,7 км/ч.
9.Ира задумала число. Если его увеличить в 4 раза, а потом результат увеличить на 7,24, то получится 35,24. Какое число задумала Ира?
Решение.
Обозначим задуманное Ирой число через х. Получаем уравнение
4х +7,24 = 35,24. Откуда х = 7.
Ответ:7.
10.*Постройте равнобедренный треугольник, если длины его боковых сторон равны 3,8 см, а градусная мера угла между ними составляет 80°.
Решение.
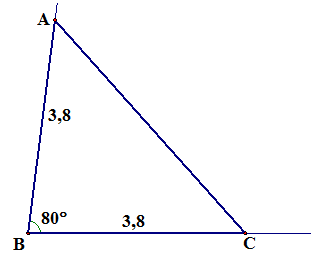
11.*Уменьшаемое увеличили на 4,7, а вычитаемое уменьшили на 1,2. В результате разность стала равной 20,6. На сколько вычитаемое было меньше уменьшаемого?
Решение.
У + 4,7 –(В – 1,2) = 20,6
У + 4,7 – В + 1,2 = 20,6
У – В = 14,7
Ответ:на14,7.
С.1.5. Сравнение десятичных дробей
1. Укажите между какими двумя последовательными натуральными числами расположена десятичная дробь 7,8:
а) 6 и 7; б) 7 и 9; в) 7 и 8; г) 8 и 9.
Ответ: в) 7 и 8.
2. Сравните:
1) 5,2300 и 5,023; 2) 1,010 и 1,001;
3) 9,20 и 9,1909; 4) 74,69800 и 74,6;
5) 6,4 и (6+3/10); 6) (29+1/25)и 29,01.
Ответ:
1) 5,2300 > 5,023; 2) 1,010 < 1,001;
3) 9,20 > 9,1909; 4) 74,69800 > 74,6;
5) 6,4 > 6,3; 6)29,04 > 29,01.
3. Запишите в порядке возрастания дроби:
1) 5,42; 5,04; 5,104; 5,509;
2) 0,44; 0,4444; 0,4; 0,444;
3) (9+9/10); 10,1; 9,099;(10+1/1000).
Ответ:
1) 5,04; 5,104; 5,42; 5,509;
2) 0,4; 0,44; 0,444; 0,4444;
3) 9,099;9,9; 10.001; 10,1.
4. Сравните:
1) 491,2 см и 4,912 м; 2) 235,4 кг и 2,354 т;
3) 6,4 ч и 388 мин; 4) 30,5 дм2 и 0,305 м2.
Ответ:
1) 491,2 см = 4,912 м; 2) 235,4 кг < 2,354 т;
3) 6,4 ч < 388 мин; 4) 30,5 дм2 = 0,305 м2.
5.* В одной коробке на (6+1/2)кг печенья больше, чем во второй. Сколько килограммов печенья во второй коробке, если в ней в 3 раза меньше печенья, чем в первой?
Решение. Пусть во второй коробке х кг печенья. Тогда х+ (6+1/2) = 3х.
Получаем: 2х = (6+1/2); 2х = 13/2; х = (13/2):2; х = 13/4;х =(4+1/4)(кг) – во второй коробке.
Ответ:4,25 кг.
Контрольная работа 1 к главе «Десятичные дроби»
Вариант 1.
1.Укажите правильный вариант чтения числа 5, 0019:
а) пять целых девятнадцать сотых;
б) пять целых девятнадцать десятых;
в) пять целых девятнадцать тысячных;
г) пять целых девятнадцать десятитысячных;
Ответ: г) пять целых девятнадцать десятитысячных.
2. Запишите в виде десятичной дроби:
1) нуль целых восемьдесят пять тысячных;
2) четыре целых двадцать одна десятитысячная;
3) триста пять целых восемь сотых;
4) три тысячных.
Ответ:1) 0,018; 2) 14,0021; 3) 305,08; 4) 0, 003.
3.Запишите в виде десятичной дроби обыкновенную дробь:
1) 7/10; 2) 23/1000; 3) (12+1/4) ; 4)(9+9/100).
Ответ:1) 0,7; 2) 0,023; 3) 12,25; 4) 9,09.
4.Запишите в виде обыкновенной дроби десятичную:
1) 0,3; 2) 0,15; 3) 0,0007;
4) 3,2; 5) 1,01; 6) 12, 121212.
Ответ:1) 3/10; 2) 15/100; 3) 7/10 000;
4)(3+1/5); 5)(1+1/100); 6)(12+121212/1000000).
5. Запишите три десятичные дроби, равные данной обыкновенной:
1) ¼; 2) 1/20.
Ответ:1) 0,25 = 0,250 = 0, 2500; 2) 0,05 = 0,050 = 0,0500.
6. Выразите:
1) в метрах:
а) 56 см; б) 3 дм 9 мм;
2) в центнерах:
а) 650 г; б) 5 кг 7 г;
3) в гектарах:
а) 650м2; б) 30м215 см2.
Ответ: 1) в метрах:
а) 56 см = 0,56 м; б) 3 дм 9 мм = 0,309м;
2) в центнерах:
а) 650 г = 0,00650 ц = 0,0065 ц; б) 5 кг 7 г = 5,05007 ц;
3) в гектарах:
а) 650м2= 0,0650 га = 0,065 га; б) 30м215 см2= 0,00300015 га.
7. Начертите координатный луч (за единичный отрезок примите 10 клеток). Отметьте на нем число:
1) 0,1; 2) 0,7; 3) 1,4.
Решение.
8. Сравните числа:
1) 2,8 и 1, 823; 2) 3, 956 и 3, 96;
3) 0,0044 и 0,01.
Ответ: 1) 2,8 > 1, 823; 2) 3, 956 < 3, 96;
3) 0,0044 < 0,01.
9. Постройте угол АОВ, градусная мера которого 140°. С помощью линейки и транспортира:
1) постройте биссектрису ОС угла АОВ;
2) разделите угол АОВ на 4 равные части.
Решение.
10.* Велосипедист проехал 1/5 пути. Ему еще осталось проехать на 12 км больше, чем он проехал. Каков весь путь?
Решение.
4/5 пути составляют 12 км,
1/5 пути = 12км: 4 = 3 км.
Весь путь равен 3 км ·5 = 15 км.
Ответ: 15 км.
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка youtube





