Решил сам
Локация Главная страница Карта сайта

Кто первым решит следующие задачи?
Задача 49.Сравните дроби 23/99, 2323/9999, 232323/999999. Ответ поясните.
Решение 1. Метод Ильи Макуцевича: если а – b = 0, то а = b.
Имеем: 23/99 – 2323/9999 = 0, 23/99 – 232323/999999 = 0. Следовательно, 23/99 =2323/9999 = 232323/999999.
Решение 2. Метод Анастасии Клебеко: если а/b = 1, то а = b.
Имеем: 23/99 : 2323/9999 = 1, 23/99 : 232323/999999 = 1. Следовательно, 23/99 =2323/9999 = 232323/999999.
Ответ: 23/99 =2323/9999 = 232323/999999.
Задача 48.Какое из чисел 7777777773/7777777778 или 8888888882/8888888887 больше? Ответ объясните.
Решение.
Задача 47.В летнем лагере 70 детей.Из них 27 занимаются в драмкружке, 32 – поют в хоре, 22 – увлекаются спортом. В драмкружке – 10 ребят из хора, в хоре – 6 спортсменов, в драмкружке – 8 спортсменов, 3 спортсмена посещают драмкружок и хор. Сколько детей не участвует ни в одном кружке? Сколько занимающихся только спортом?
Решение.
Задача 46.Сравните две дроби: 1993/1994 и 1993000001993/1994000001994. Ответ объясните.
Решение.
Задача 45.Делится ли число 11·21·31·41·51·61·71·81·91 – 1 на 10? Почему?
Решение. (Манкевич Сергей)
Так как произведение 11·21·31·41·51·61·71·81·91 оканчивается 1, то разность 11·21·31·41·51·61·71·81·91 – 1 оканчивается 0. Значит, по признаку делимости на 10, данное число делится на 10.
Задача 44.Укажите последнюю цифру, которой заканчивается значение выражения 72005+92005?
Решение.
Задача 43.Вычислите значение суммы
1/(1·2)+1/(2·3)+1/(3·4)+1/(4·5)+1/(5·6)+1/(6·7)+1/(7·8)+1/(8·9)+1/(9·10).
Решение.
Задача 42.У Змея Горыныча 2010 голов. Иван-царевич может срубить ему одним ударом меча 21, 17 или 1 голову, но при этом у него вырастает взамен 0, 14, 49 голов соответственно. Если отрублены все головы, то новых голов не вырастает. Сможет ли Иван-царевич одолеть Змея Горыныча?
Решение.
Задача 41*. 1) Постройте замкнутую ломаную из 3 звеньев и проходящую через 4 данные точки, не отрывая карандаша от бумаги.

2) Как ломаной линией, состоящей из 4 отрезков, не отрывая карандаша от бумаги, перечеркнуть девять точек?
Решение.Первой решила Ксения Бильмон
1)
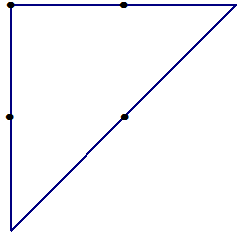
2)
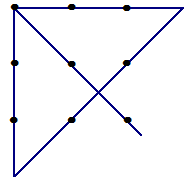
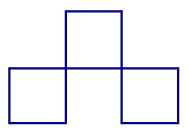
Задача 40*. Из 12 спичек построено 4 равных квадрата

Как переложить 3 спички, чтобы получились три равных квадрата?
Решение.
Задача 39*.Расставьте скобки так, чтобы равенство 13 – 4:3 + 2·5 – 1 = 11 было верным.Первыми решили Антоний Седеневский и Никита Сигатов
Ответ: (13 – 4):3 + 2·(5 – 1) = 11.
Задача 38*. Имеется 10 гирек: 4 гирьки массой 1 г, 3 гирьки массой 2г, 2 гирьки массой 3 г и одна гирька массой 4 г. 1) Можно ли разложить эти гирьки на четыре кучки так, чтобы общая масса каждой кучки была одна и та же? 2) Можно ли разложить эти гирьки на три кучки так, чтобы общая масса каждой кучки была одной и той же?
Решение.(Манкевич Сергей) 1) На четыре кучки разложить можно, так как 4+6+6+4 = 20 делится на 4 и 20:4 = 5. Например , так: 2+3, 4+1, 2+3, 1+1+1+2. 2) Разложить на три кучки нельзя, поскольку 4+6+6+4 = 20 не делится на .
Задача 37*. Пять двоек записаны в ряд. Вставляя между некоторыми из них знаки арифметических действий и скобки, можно получить различные числа, например, 14 = (2 + 2 + 2)·2 + 2. Как получить число: а) 9; б) 13; в) 113?
Задача 36*. Назовите последнюю цифру произведения всех трехзначных чисел, которые не делятся на 2.Первым решил Александр Клемято
Решение.
Не делятся на 2 трехзначные числа: 101, 103, 105, 107, 109, 111,…, 999.. Все они нечетные и среди них есть те, которые оканчиваются 5. При умножении на 5 любого нечетного множителя их произведение будет оканчиваться на 5. Значит, и произведение данных чисел будет оканчиваться цифрой 5.
Ответ: 5.
Задача 35*. Какой цифрой оканчивается разность
1·2·3·…·21·22 – 1·3·5·…·13·15 ?
Решение. (Манкевич Сергей) Уменьшаемое оканчивается 0, а вычитаемое - 1, следовательно, разность оканчивается 5.
Задача 34*. Сколько имеется пятизначных чисел, у которых сумма цифр не делится на 2?Первым решил Илья Макуцевич
Решение.
Рассмотрим пятизначные числа, удовлетворяющие условию задачи:
10 000, 10 002, 10 004, 10 006, 10 008, 10 011, 10 013, 10 15, 1017, 10 019, …, 99 999. В каждом десятке по 5 чисел, в каждой сотне – 5·10 = 50, в каждой тысяче – 50 · 10 = 500, а тысяч всего 90, так как 99 999 – 9 999 = 90 000. Следовательно, число всех искомых пятизначных чисел равно 500·90 = 45000.
Ответ: 45 000.
Задача 33*.Поставьте вместо звездочек знаки арифметических действий «+», «-», «·», «:» так, чтобы значение выражения 76*4*51*3 было равно 36.Первыми решили Никита Сигатов и Денис Петько
Решение.
76:4 + 51:3 = 19 + 17 = 36.
Ответ:76:4+51:3.
Задача 32*. Если к некоторому двузначному числу приписать справа 0, то оно увеличится на 504. Найдите это число.Первым решил Антоний Седеневский
Решение.
Пусть х – искомое двузначное число. Приписать справа нуль к нему – это значит увеличить его в 10 раз. По условию 10х = х+ 504. Откуда получаем: 10х – х= 504, 9х = 504, х = 56.
Ответ:56.
Задача 31*.
Задача 30*. В двух сумках лежат 100 огурцов. Может ли число огурцов в одной из сумок быть в два раза больше , чем в другой?
Решение.(Манкевич Сергей) Так как в одной сумке 2 части, а в другой 1 часть, то 100 не делится на 3, следовательно, число огурцов в одной из сумок быть в два раза больше , чем в другой не может.
Задача 29*. Из восьми одинаковых колец одно несколько легче остальных. Найдите его при помощи не более чем двух взвешиваний на чашечных весах.Первым решил Никита Сигатов
Решение.
Положим на каждую чашку весов по три кольца из данных.
Возможны 2 случая:
1) Весы в равновесии. Следовательно, более легкое кольцо среди двух оставшихся. Вторым взвешиванием находим более легкое кольцо так: положив на каждую чашку по одному кольцу из оставшихся после первого взвешивания, заметим, которая чашка весов опустилась. В ней и будет более легкое кольцо.
2) При первом взвешивании опустилась одна из чашек с тремя кольцами. Это значит, что именно в ней среди трех колец одно более легкое. Из этих трех колец возьмем любые 2 и положим их по одному на обе чашки весов. Если весы в равновесии, то более легкое кольцо оставшееся. Если какая-то чашка при взвешивании опустилась, то более легкое кольцо находится в ней.
Значит, в любом случае можно определить кольцо, которое несколько легче остальных, не более чем двумя взвешиваниями.
Задача 28*. У картонного квадрата отрезали 3 угла. Сколько углов осталось?Первым решил Антоний Седеневский
Решение.
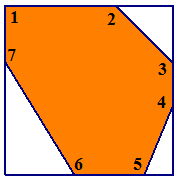
Ответ: 7.
Задача 27*. Дед в 2 раза сильнее бабки. Бабка в 3 раза сильнее внучки. Внучка в 5 раз сильнее Жучки, Жучка в 7 раз сильнее кошки, а кошка в 10 раз сильнее мышки. Сколько нужно позвать мышек, чтобы вытянуть репку?Первым решил Артур Кислый
Решение.
1 кошка равна по силе 10 мышкам, т. е. 1 кошка = 10 мышек.
1 Жучка = 7 кошек = 70 мышек.
1 внучка = 5 Жучек = 350 мышек.
1 бабка = 3 внучки = 1050 мышек.
1 дед = 2 бабки = 2100 мышек.
Вместе имеем: 2100 +1050 + 350 + 70 + 10 +1 = 3581 мышка.
Ответ: 3581 мышка.
Задача 26*. Сколько существует трехзначных чисел, цифры которых –нечетные и никакие цифры не повторяются внутри одного числа?
Решение.Первой решила Ольга Тулько
Мы можем воспользоваться пятью цифрами: 1, 3, 5, 7, 9. На первом месте в числе может стоять любая из них (5 вариантов). На втором месте может стоять любая из четырех оставшихся цифр. У каждого из пяти вариантов появилось по 4 варианта продолжения: 5·4 = 20(вариантов). На последнем месте может стоять любая из трех оставшихся цифр: 20·3 = 60. Можно записать 60 чисел.
Здесь мы имели дело с комбинаторными вычислениями. Мы подсчитали, сколько комбинаций можно составить из заданных цифр по три. Это была комбинаторная задача. Область математики, в которой изучаются комбинаторные задачи, называется комбинаторикой. В комбинаторике имеет место правило умножения:
5·4·3 = 60.
Ответ: 60.
Задача 25*. Какой вес можно отмерить гирями 1, 2, 4 и 8 г, если класть гири только на одну чашу весов?Первой решила Елизавета Олехнович
Решение.
Можно отмерить любой вес, не превышающий 15 г: 1, 2, 1 + 2 = 3, 4, 1+ 4 = 5, 2 + 4 = 6, 1+ 2 + 4 = 7, 8, 1+ 8 = 9, 2 + 8 = 10, 1+ 2 + 8 = 11, 4 + 8 = 12, 1+ 4 + 8 = 13, 2 + 4 + 8 = 14, 1+ 2 + 4 + 8 = 15.
Ответ: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.
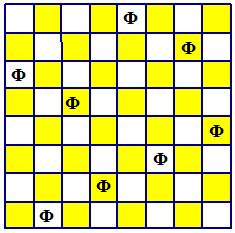
Задача 24*.Найдите такое расположение восьми ферзей на шахматной доске, при котором ни один ферзь не бьет другого.Первыми решили Алексей Куц и Алексей Микша
Решение.
Вспомнив, как ходит ферзь, приходим к выводу, что на каждой горизонтали и вертикали шахматной доски должен находиться ровно один ферзь и на любой диагонали не может стоять два ферзя. С помощью небольшого перебора находим нужное расположение:
Задача 23*. Крестьянка продавала на рынке яйца. Первая покупательница купила у нее половину яиц и еще пол-яйца, вторая половину остатка и еще пол-яйца, а третья последние 10 яиц. Сколько яиц принесла крестьянка на рынок?
Решение.
Ответ:
Задача 22*. В клетке сидят фазаны и кролики. У них вместе 35 голов и 94 ноги. Сколько фазанов и сколько кроликов в клетке?
Решение.(Манкевич Сергей)Если все кролики встанут на задние лапы, то всего лап будет 2х35=70. Значит, кроликов имеется (94-70):2=12, а фазанов 35 - 12 = 23.
Ответ:12 кроликов и 23 фазана.
Задача 21*.1 февраля был четверг. Каким днем недели было 1 марта?
Решение.Первым решил Александр Клемято
Если год невисокосный, то между 1 февраля и 1 марта ровно 4 недели (28 дней), и, значит, 1 марта – четверг. Если год високосный, то между 1 февраля и 1 марта 29 дней и тогда 1 марта – пятница.
Ответ: в високосный год пятница, в невисокосный четверг.
Задача 20*.Петя нашел один гриб, Коля – два, а Паша – три. Мама дала им 18 орехов и велела разделить их по заслугам. Сколько орехов получил каждый?
Решение 1.Первым решил Александр Клемято
Мальчики нашли 6 грибов. Паша нашел половину всех грибов, значит, ему положено взять половину всех орехов: 18:2 = 9 (орехов). Петя нашел 1/6 часть всех грибов и ему полагается шестая часть орехов: 18 : 6 = 3 (ореха). Остальные орехи должен взять Коля: 18 – 9 – 3 = 6 (орехов).
Решение 2. Грибов всего собрано 6. На каждый гриб приходится 18:6= 3(ореха). Следовательно, Петя получает 3 ореха, Коля – 3·2 = 6 (орехов), а Паша – 3·3 = 9 (орехов).
Ответ: Петя получил 3 ореха, Коля – 6, Паша – 9.
Задача 19*. Найдите сумму всех натуральных чисел от 1 до 100 включительно. Великий немецкий математик Карл Гаусс решил эту задачу за одну минуту в шестилетнем возрасте
Решение.Первым решил Александр Клемято
- Карл, расскажи классу, как ты решил эту задачу, - обратился к нему учитель.
Карл сказал:
- Я заметил, что числа данного ряда, стоящие на одинаковом расстоянии от концов, имеют одинаковую сумму. Пользуясь этим свойством, я складываю попарно 100 + 1, 99 +2, 98 + 3 и т.д., что дает каждый раз в сумме 101. Но таких пар, очевидно, 50. Следовательно, вся сумма 101 · 50 = 5050.”
Ответ: 5050.
Задача 18*.В теннисном турнире участвовали 5 школьников: Ваня, Петя, Саша, Миша и Гриша. За 3 дня Ваня сыграл 4 партии, Петя – 3, Гриша – 1. По сколько партий сыграли за это время Саша и Миша, если между собой они не играли?
Решение 1.Первым решил Александр Клемято
Будем решать задачу с помощью графа.
Изобразим школьников точками. Если два игрока встречались, то точки, им соответствующие, соединим линией.
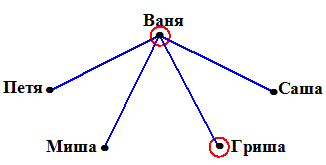
1) Ваня сыграл со всеми (красный кружок означает, что все партии, проведенные Ваней, отмечены на графе).
2) Гриша сыграл единственную партию, которая учтена (красный кружок).
3) Петя сыграл 3 партии, но только одна из них, с Ваней, учтена. Следовательно, Петя сыграл еще с Мишей и Сашей. Отметим это на рисунке:
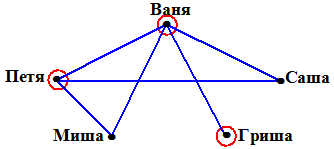 Решение 2.
Решение 2.
Поскольку Ваня сыграл со всеми по разу, а Гриша только с Ваней, то Петя должен сыграть (три партии) не только с Ваней, но и с Мишей, и с Сашей. Но тогда получается, что Миша сыграл две партии (с Ваней и с Петей) и Саша сыграл две партии (с Ваней и с Петей).
Ответ: по две партии.
Задача 17*. Как, имея лишь два сосуда вместимостью 5 л и 7 л, а также сливную раковину, налить из водопроводного крана 6 л?Первым решил Александр Клемято
Решение 1.
1) Наполним 7-литровый сосуд (1 шаг), а потом из него наполним 5-литровый сосуд(2 шаг). В 7-литровом останется 2 л воды, из 5-литрового выльем в раковину(3 шаг). В таблице это будет выглядеть так:
| | 1шаг | 2шаг | 3шаг | 4шаг | 5шаг | 6шаг | 7шаг | 8шаг | 9шаг | 10шаг |
| 7-л | 7 | 2 | 2 | 0 | 7 | 4 | 4 | 0 | 7 | 6 |
| 5-л | 0 | 5 | 0 | 2 | 2 | 5 | 0 | 4 | 4 | 5 |
2) Эти 2 л из 7-литрового сосуда перельем в 5-литровый сосуд(4 шаг), а 7-литровый наполним вновь(5 шаг).
3) Из 7-литрового сосуда нальем в 5-литровый (6 шаг), в котором 2 л уже есть, еще 3 л, в 7-литровом останется 4 л.
4) Из 5-литрового сосуда все выльем в раковину (7 шаг), а 4 л из 7-литрового сосуда перельем в 5-литровый (8 шаг).
5)Наполним 7-литровый сосуд (9 шаг), а затем в 5-литровый сосуд, в котором 4 л есть, дольем еще 1 л. В 7-литровом сосуде останется 6 л (10 шаг), т. е. в нем окажется 6 л, что и требовалось сделать.
Решение 2.
| | 1шаг | 2шаг | 3шаг | 4шаг | 5шаг | 6шаг | 7шаг | 8шаг | 9шаг | 10шаг |
| 7-л | 0 | 5 | 7 | 0 | 3 | 3 | 7 | 0 | 1 | 6 |
| 5-л | 5 | 5 | 3 | 3 | 0 | 5 | 1 | 1 | 5 | 0 |
Задача 16*.С числом, записанным на доске, разрешены следующие операции: либо заменять его удвоенным, либо стирать его последнюю цифру. Как с помощью этих операций из числа 458 получить 14?
Решение 1.Первой решила Ольга Ледакович
1) 458·2 = 916 (удвоили)
2) 91 (стерли последнюю цифру)
3) 91·2 = 182 (удвоили)
4) 18 (стерли последнюю цифру)
5) 18· 2 = 36 (удвоили)
6) 36·2 = 72 (удвоили)
7) 7 (стерли последнюю цифру)
8) 7·2 = 14 (удвоили и получили требуемое)
Решение 2.
1) Заменяем данное число удвоенным: 458·2 = 916.
2) Стираем в полученном числе последнюю цифру: 91.
3) Заменяем полученное число удвоенным: 91·2 = 182.
4) Стираем в нем последнюю цифру: 18.
5) Заменяем полученное число удвоенным: 18·2 = 36.
6) Заменяем полученное число удвоенным: 36·2 = 72.
7) Заменяем полученное число удвоенным: 72·2 = 144.
8) Стираем последнюю цифру: 14, что и требовалось получить.
Задача 15*.Из 52 учеников 23 собирают значки, 35 – марки, а 16 – и значки, и марки. Сколько учеников не увлекается коллекционированием?Первыми решили Ольга Ледакович и Сергей Манкевич
Решение.
1) 23 – 16 = 7 (учеников) – собирают только значки.
2) 35 + 7 = 42 (ученика) – увлекаются коллекционированием.
3) 52 – 42 = 10 (учеников) – не увлекаются коллекционированием.
Ответ: 10.
Задача 14*. Верно ли, что сумма 1 + 2 + 3 + … + 2009 делится на 2009? Первым решил Александр Клемято
Решение.
1 + 2 + 3 + … +2008 + 2009 = (1+2008)·1004 +2009 = 2009·1005, т. е. данная сумма делится на 2009.
Ответ:верно.
Задача 13*. Во владениях Снежной Королевы 12 ледяных домиков и каждые два домика соединены дорогой. Сколько дорог в королевстве?Первым решил Александр Клемято
Решение.
1) 1-ый домик соединим дорогами с каждым из остальных 11 домиков и получим 11 дорог.
2) 2-ой домик уже соединен дорогой с 1-ым. Соединим его дорогами с каждым из остальных 10 домиков и получим еще 10 дорог.
3) 3-й домик осталось соединить дорогами с 4, 5, 6, 7, 8, 9, 10, 11 и 12 домиками. Это еще 9 дорог.
4) 4-й домик осталось соединить дорогами с 5, 6, 7, 8, 9, 10, 11 и 12 домиками. Это еще 8 дорог.
5) 5-й домик осталось соединить дорогами с 6, 7, 8, 9, 10, 11 и 12 домиками. Это еще 7 дорог.
6) 6-й домик осталось соединить дорогами с 7, 8, 9, 10, 11 и 12 домиками. Это еще 6 дорог.
7) 7-й домик осталось соединить дорогами с 8, 9, 10, 11 и 12 домиками. Это еще 5 дорог.
8) 8-й домик осталось соединить дорогами с 9, 10, 11 и 12 домиками. Это еще 4 дороги.
9) 9-й домик осталось соединить дорогами с 10, 11 и 12 домиками. Это еще 3 дороги.
10) 10-й домик осталось соединить дорогами с 11 и 12 домиками. Это еще 2 дороги.
11) 11-й домик осталось соединить дорогой с 12 домиком. Это еще 1 дорога.
12) После этого каждые два домика оказались соединенными дорогами, а число дорог равно сумме:
11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 11 + 55 = 66.
Ответ:66.
Задача 12*.На поляне собрались: Попугай, Удав, Слоненок, Теленок, Котенок, Мартышка и Верблюженок. Попугай начал всех измерять. Оказалось, что Слоненок длиннее Теленка на 3 Попугая, Верблюженок длиннее Мартышки тоже на 3 Попугая, Теленок длиннее Попугая на 7 Попугаев, Верблюженок длиннее Котенка на 6 Попугаев, а все они укладываются в точности на Удаве, длина которого 38 Попугаев. Найдите длину каждого в Попугаях.
Решение. (Манкевич Сергей) Теленок равен 1 + 7 = 8 Попугаев. Слоненок равен 8+3 = 11 Попугаев. Следовательно, Котенок+Мартышка+Верблюженок=38-1-8-11=18 Попугаев. Мартышка = Верблюженок - 3 Попугая, Котенок = Верблюженок - 6 Попугаев. Так как Верблюженок +Верблюженок-3+Верблюженок-6=18, то Верблюженок = 9 Попугаев, Мартышка - 6 Попугаев, Котенок - 3 Попугая.
Ответ: длины в Попугаях: Теленок - 8, Слоненок - 11, Котенок - 3, Верблюженок - 9, Мартышка - 6.
Задача 11*.Незнайка неправильно списал с доски условие примера на сложение нескольких чисел. В одном из слагаемых вместо цифры единиц 5 он написал 8, в другом – вместо цифры десятков 4 он написал 9 и в одном из оставшихся слагаемых цифру сотен 3 принял за 1. В сумме получилось 55 561. Найдите верную сумму.
Решение.Первыми решили Анастасия Клебеко и Андрей Кишкель
1) 8 – 5 = 3(ед.) – на столько единиц новая сумма больше старой.
2) 9 – 4 = 5 (дес.) – на столько десятков новая сумма больше старой.
3) 3 – 1 = 2(сотни) – столько сотен не хватает в верной сумме.
4) 55 561 – 3 – 50 + 200 = 55 708 – верная сумма.
Ответ: 55 708.
Задача 10*.От дачного участка до железнодорожной станции и обратно дачник на велосипеде едет 24 мин. Если он до станции поедет на велосипеде, а назад пойдет пешком, то затратит 42 мин. За какое время дачник пройдет путь пешком от дачи до станции и обратно?Первым решил Андрей Кишкель
Решение.
1) 24 : 2 = 12 (мин) – столько времени дачнику нужно для проезда в одну сторону на велосипеде.
2) 42 – 12 = 30 (мин) – столько времени нужно дачнику на путь пешком в одну сторону.
3) 30 ·2 = 60 (мин) = 1 (ч) – столько дачнику нужно на путь пешком туда и обратно.
Ответ:1ч.
Задача 9*.Петя задумал натуральное число меньшее 100. Покажите, что вы можете определить это число, задав Пете не более 7 вопросов, на которые он будет давать ответы словами «да» или «нет».
Решение.Первым решил Александр Клемято
Пусть Петя задумал самое большое из данных натуральных чисел – 99 (нечетное). Как его определить, задав Пете не более 7 вопросов?
1) Является ли число четным? Ответ: нет
Осталось рассмотреть 50 нечетных чисел.
2) Получится ли остаток 1 при делении числа на 4? Ответ: нет.
Осталось рассмотреть 25 чисел при делении на 4 дающих остаток 3: 3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71, 75, 79, 83, 87, 91, 95, 99.
3) Получится ли остаток 3 при делении числа на 8? Ответ: да.
Следовательно, поиск ведем среди 13 чисел: 3, 11, 19, 27, 35, 43, 51, 59, 67, 75, 83, 91, 99.
4) Получится ли остаток 3 при делении на 16? Ответ: да.
Значит, искомое число находится среди 7 чисел: 3, 19, 35, 51, 67, 83, 99.
5) Получится ли остаток 3 при делении числа на 32? Ответ: да.
Остается 4 числа: 3, 35, 67, 99.
6) Получится ли остаток 3 при делении числа на 64? Ответ: нет.
Остается 2 числа: 35 и 99.
7) Является ли число 35 ответом? Ответ: нет.
В таком случае искомым является число 99.
Аналогичные рассуждения будут и в случае других задуманных нечетных чисел, и в случае ответа «да» на первый вопрос, т. е. когда задумано какое-либо четное число.
Задача 8*. Почтальон Печкин получил для продажи несколько пачек конвертов по 100 штук в пачке. За какое наименьшее число секунд он может выдать 60 конвертов, если 10 конвертов он отсчитывает за 10 секунд? А 90 конвертов?Первой решила Илона Жебрик
Решение.
В первом случае почтальон Печкин может отсчитать за 40 секунд 40 конвертов и сразу выдать 60 оставшихся в пачке конвертов. Во втором случае за 10 секунд он может отсчитать 10 конвертов и сразу выдать оставшиеся в пачке 90 конвертов.
Ответ:40 секунд, 10 секунд.
Задача 7. Три утенка и четыре гусенка имеют массу 2 кг 500 г, а четыре утенка и три гусенка – 2 кг 400 г. Какова масса одного гусенка?
Решение.Первыми решили Ольга Ледакович и Сергей Манкевич
1) 2 кг 500 г + 2 кг 400 г = 2500 г + 2400 г = 4900 г – масса семи утенков и семи гусенков.
2) 4900 : 7 = 700 (г) – масса одного утенка и одного гусенка.
3) 700 · 3 = 2100 (г) – масса трех утенков и трех гусенков.
4) 2500 – 2100 = 400 (г) – масса одного гусенка.
Ответ: 400 г.
Задача 6. Три феи пришли на бал в розовом, голубом и белом платьях. Их туфли были тех же цветов. У первой феи цвета платьев и туфель совпадали. У второй феи ни туфли, ни платья не были розовыми, а у третьей – голубые туфли и платье другого цвета. Как были одеты феи?
Решение.Первыми решили Ольга Ледакович и Сергей Манкевич
Внесем сведения «У второй феи ни туфли, ни платья не были розовыми, а у третьей – голубые туфли и платье другого цвета» в таблицу (то, что не было отмечаем знаком -, а то что было знаком +):
| Платья | Туфли | ||||
Розовое | Голубое | Белое | Розовые | Голубые | Белые | |
1 фея |
|
|
|
| - |
|
2 фея | - |
|
| - | - |
|
3 фея |
| - |
| - | + | - |
Так как у второй и третьей фей туфли не розовые, то розовые туфли у первой феи. Тогда белые туфли у второй феи. Внесем это в таблицу:
| Платья | Туфли | ||||
Розовое | Голубое | Белое | Розовые | Голубые | Белые | |
1 фея |
|
|
| + | - | - |
2 фея | - |
|
| - | - | + |
3 фея |
| - |
| - | + | - |
«У первой феи цвета платьев и туфель совпадали». Значит, у первой феи платье розовое. Тогда у первой и третьей фей платье не голубое, следовательно, оно голубое у второй феи. Белое платье остается третьей фее. Окончательно таблица примет вид:
| Платья | Туфли | ||||
Розовое | Голубое | Белое | Розовые | Голубые | Белые | |
1 фея | + | - | - | + | - | - |
2 фея | - | + | - | - | - | + |
3 фея | - | - | + | - | + | - |
Ответ: у первой феи платье и туфли розовые, у второй феи платье голубое, а туфли белые, у третьей феи платье белое, а туфли голубые.
Задача 5. Мальчик строит квадратики. Ежедневно он достраивает квадратик, полученный накануне, до большего.
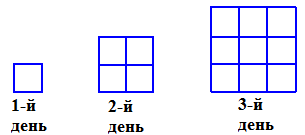
Сколько маленьких квадратиков в квадрате, построенном на 10-й день?
Решение.Первым решил Сергей Манкевич
В первый день построенная мальчиком фигура состоит из 1 квадратика, во второй день – из 4-х, в третий – из 9. Эти числа можно представить в таком виде: 1 = 1·1, 4 = 2·2, 9 = 3·3. Число квадратиков равно произведению числа квадратиков в одном ряду на число рядов. Число квадратиков в квадрате, построенном на 10-й день, равно 10·10 = 100.
Ответ: 100.
Задача 4. Разрежьте квадрат на 4 части, и сложите из этих частей 3 квадрата (все части должны быть использованы).
Решение.Первым решил Владислав Жебрик

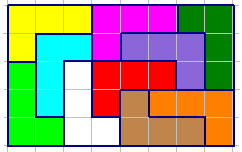
Задача 3.Разрежьте данный прямоугольник на фигуры указанного вида:
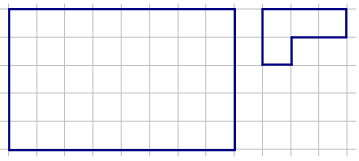
Решение.Первыми решили Илья Макуцевич и Сергей Манкевич
Задача 2*.Набор состоит из 30 гирек массами 1 г, 2 г, 3 г, …, 30 г. Можно ли эти гирьки разложить на группы по 10 штук так, чтобы масса всех гирек в каждой группе была одной и той же?
Решение Первым решил Алексей Жинко
Масса всех 30 гирек равна (1+30)·15 = 465. Значит, масса каждой из трех групп – это 465:3 = 155 (г). Сложим отдельно массы первых десяти гирек, затем следующих 10 и, наконец, последних 10 гирек. Соответственно получим (1 +10)·5 = 55(г), (11 + 20)·5 = 155 (г), (21 + 30)·5 = 255(г). Таким образом, средняя группа удовлетворяет условию. Осталось перераспределить гирьки между первой группой (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) и последней (21, 22, 23,24, 25, 26, 27, 28, 29, 30). Заметим, 1 + 30 = 2 + 29 = 3 + 28 = 4 +27 = 5 + 26 = 31. Поскольку 31·5 = 155, то теперь ясно, какие группы получатся:
1) 1, 2, 3, 4, 5, 26, 27, 28, 29, 30;
2) 11, 12, 13, 14, 15, 16, 17, 18, 19, 20;
3) 6, 7, 8, 9, 10, 21, 22, 23, 24, 25.
Ответ: можно
Задача 1. Замените буквы цифрами (одинаковым буквам соответствуют одинаковые цифры, разным буквам – разные цифры): ЛЕТО + ЛЕТО = ПОЛЕТ. В качестве ответа представьте пятизначное число, соответствующее слову ПОЛЕТ.Первыми решили Илона Жебрик и Сергей Манкевич
Решение.
ЛЕТО
+ЛЕТО
ПОЛЕТ
Заметим, что сумма последних цифр слагаемых (О + О) равна предпоследней цифре слова ЛЕТО, т. е. Т. Далее Т+Т=Е, Е+Е=Л, Л+Л=О+1. Следовательно, задачу можно решить перебором, подставляя вместо буквы О последовательно все цифры от 0 до 9 .
1) 0+0=0(О =Т) – не подходит.
2) 1+1=2(О=1,Т=2), 2+2=4(Е=4), 4+4=8(Л=8), 8+8=16(О = 6 и О = 1) – не подходит.
3) 2+2=4(О=2,Т=4), 4+4=8 (Е=8), 8+8=16(Л=6), 6+6+1=13 (О = 3 и О = 1) – не подходит.
3) 3+3=6(О=3, Т=6), 6+6=12(Е=2), 2+2+1=5(Л=5), 5+5=10(О=3 и О=0) – не подходит.
4) 4+4=8(О=4,Т=8), 8+8=16(Е=6), 6+6+1=13(Л=3), 3+3=6(О=4 и О=6) – не подходит.
5) 5+5=10(О=5,Т=0), 0+0=0(Е=0 и Т=0) – не подходит.
6) 6+6=12(О=6,Т=2), 2+2+1=5(Е=5), 5+5=10(Л=0), 0+0+1=1(О=1 , П=0) – не подходит.
7) 7+7 = 14(О=7, Т=4), 4+4+1=9(Е=9), 9+9=18(Л=8), 8+8+1=17(О=7,П=1), т. е.
8 947+8 974=17 894 – верно.
8) 8+8=16(О=8, Т=6), 6+6+1=13(Е=3), 3+3=6(Л=6 и Т=6) – не подходит.
9) 9+9=18(О=9,Т=8), 8+8+1=17(Е=7), 7+7+1=15(Л=5), 5+5+1=11(О=1 и О=8) – не подходит.
Ответ:17 894.
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка инстаграм