vivat2.okis.ru

Локация Главная страница Карта сайта

Весомость заданий Шкала перевода баллов Продолжение шкалы перевода

Прототипы задания 3 профиля ЕГЭ - 2021(№ 8,15 базового уровня)

Тема заданий № 3  "Квадратная решетка. Координатная плоскость"

Типы заданий № 3: многоугольники: вычисление длин и углов здесь и здесь и здесь многоугольники: вычисление площадей здесь и здесь и здесь и здесь круг и его элементы здесь и здесь координатная плоскость здесь и здесь

Вид задания: с кратким ответом. Уровень сложности: базовый. Количество баллов: 1. Примерное время на выполнение: 2 минуты. Средний процент выполнения: в 2019 году 93,3%, в 2020 году 89,8%. Ответом к заданию 3 по математике может быть целое число или конечная десятичная дробь. Требования ФИПИ к профильному уровню  здесь Соответствие заданий в КИМах базового и профильного уровня здесь

За  заданием № 3  негласно закрепилось название «фигура на бумаге в клетку». В этом задании  чаще всего представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге. Большая часть заданий этого типа являются несложными, однако объем теоретического материала, которым надо владеть, достаточно обширен. Определения, теоремы и формулы следует выучить и постоянно повторять, проверяя себя. В заданиях № 3 содержатся основы геометрии. Чаще всего здесь встречаются задания на решение треугольников, но знать надо все фигуры планиметрии:  виды треугольников здесь здесь  понятия биссектрисы, медианы, высоты здесь тригонометрические функции и их значения здесь здесь  основное тригонометрическое тождество здесь формулы приведения здесь теорема Пифагора и теорема косинусов здесь четырехугольники здесь здесь здесь  правильный шестиугольник здесь площади многоугольников  здесь здесь окружность здесь здесь здесь здесь здесь здесь здесь здесь круг и его элементы здесь площадь круга здесь площадь кругового сектора здесь площадь кольца здесь векторы здесь здесь здесь здесь здесь

Тригонометрические функции острого угла прямоугольного треугольника– это не только часть планиметрических задач №3 и №6, но и ряд задач про геометрический смысл производной (№7), задачи, где требуется вычислить значения тригонометрических функций (№9 и даже №10).

В заданиях №3 встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг. При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки – надо внимательно читать задание. По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.

Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.

При подготовке полезно пользоваться  справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку. Определения, а также свойства фигур и их элементов, в справочных материалах на ЕГЭ не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.

Сложных вычислений в третьем задании нет. Бывают задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще. Большинство задач можно решить несколькими способами.

Чтобы решить задание 3 необходимо: 1. Уметь вычислять площадь фигуры, 2. Уметь вычислять градусные меры углов, 3. Уметь вычислять периметры, 4. Знать, что длина средней линии трапеции находится по формуле l= (a+b)/2 5. Знать, что можно воспользоваться формулой Пика S = В + Г/2 - 1 , где S - площадь многоугольника, В - количество узлов сетки, лежащих внутри многоугольника, Г - количество узлов сетки, лежащих на границе многоугольника здесь

Тесты. Вычисление углов: 1) здесь ответ 2) здесь ответ 3) здесь решение 4) здесь решение 5) здесь решение 6) здесь решение 7) здесь решение 8) здесь решение 9) здесь решение 10) здесь решение 11) здесь решение 12) здесь здесь Вычисление длин: 1) здесь решение 2) здесь решение 3) здесь решение 4) здесь решение 5) здесь здесь 6) здесь решение 7) здесь решение Вычисление площадей: 1) здесь  решение 2) здесь  решение 3) здесь решение 4) здесь  решение 5) здесь решение 6) здесь решение 7) здесь  здесь 8) здесь решение 9) здесь решение 10) здесь  решение 11) здесь здесь 12) здесь здесь Вычисление элементов круга: 1) здесь решение 2) здесь решение 3) здесь решение 4) здесь  решение 5) здесь решение  6)здесь решение 7) здесь решение 8)здесь решение 9)здесь   решение 10) здесь решение 11) здесь решение 12) здесь здесь 13) здесь решение 14) здесь решение 15) здесь решение 16) здесь решение 17) здесь решение Вычисления на координатной плоскости: 1)здесь  решение 2) здесь  решение 3) здесь решение 4) здесь решение 5) здесь решение 6) здесь решение 7) здесь решение 8) здесь  решение 9) здесь решение 10) здесь решение 11) здесь решение 12) здесь решение 13) здесь решение  14) здесь решение 15)  здесь решение 16) здесь решение

Вы обязательно завалите задачу № 3, если не читая ее условие, просто посчитаете площадь и запишете полученное число в ответ. И потом будете недоумевать почему Вам поставили 0 баллов до тех пор, пока  не увидите,  что в ответе нужно было указать среднюю линию, медиану или тангенс угла.

Задачи с ответами для самостоятельного решения и  самопроверки,

предлагаемые авторами ЕГЭ на экзаменах прошлых лет, а также из открытого банка ФИПИ: 

1. 2021 год. Демонстрационный вариант ЕГЭ. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

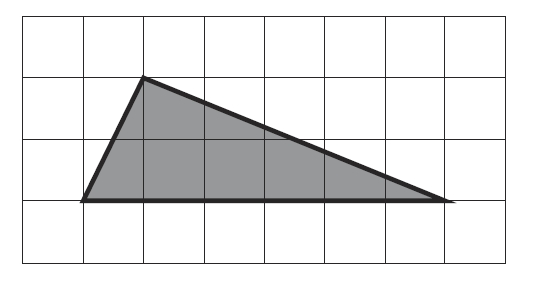 Решение здесь

ИЛИ

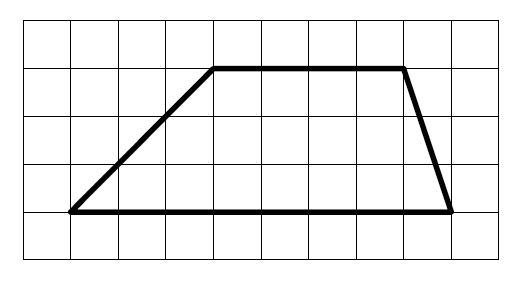
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции. Решение здесь

1. 2020 год. Основная волна. Москва. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение здесь или здесь Ответ:15.

2. 2020 год. Досрочная волна.

На клетчатой бумаге с размером 1х1 изображён ромб. Найдите его площадь.

Решение 1 здесь Решение 2 здесь

3. 2019 год. Основная волна ЕГЭ. Центр. Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1×1 см. Ответ дайте в квадратных сантиметрах.

Решение здесь

4. 2018 год. Основная волна ЕГЭ. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите среднюю линию этой трапеции.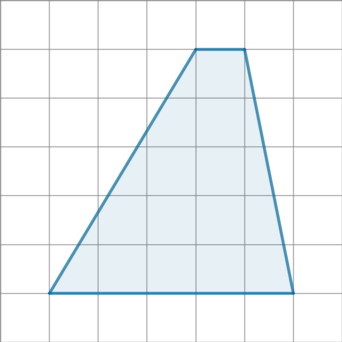

   Решение здесь

5. 2017 год. Основная волна ЕГЭ.  На клетчатой бумаге изображен треугольник ABC. Найдите среднюю линию этого треугольника, параллельную стороне AB.

Решение здесь

6. 2016 год. Основная волна ЕГЭ. Юг. На клетчатой бумаге с размером клетки 1х1 изображен параллелограмм. Найдите его площадь.

Основание параллелограмма 2, высота 5. Ответ: здесь

5. Найдите площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1см х 1 см (см. рис.). В ответе запишите S/п.

 Решение здесь

6. Найдите площадь S круга, считая стороны квадратных клеток равными 1 (см. рис.).  В ответе укажите S/п.

 Решение здесь

Вероятно, вы привыкли, что в задании № 3 в профильном ЕГЭ необходимо найти площадь или хотя бы периметр. Однако это не всегда так. В последнее время этим заданием стали проверять ваше знание базовых элементов и теорем геометрии, поэтому просят найти медиану, высоту, биссектрису, среднюю линию или радиус окружности. Чтобы выполнить это задание верно, необходимо внимательно читать условие и иметь в голове всю теорию в структурированном виде, чтобы вовремя воспользоваться нужным правилом.

7. На клетчатой бумаге с размером клетки 1х1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведенной к гипотенузе.

 Решение здесь

8.   Найдите большую диагональ ромба.

 Решение здесь

9. Найдите площадь треугольника.

 Решение здесь 

Задачу 5 можно решить и другим способом здесь

10. Найдите площадь многоугольника

  Решение здесь 

Задачу 6 можно решить и вычитанием из площади прямоугольника здесь

11. Найти площадь многоугольника.

 Решение здесь 

12. Найдите градусную меру угла АВС.

  Решение здесь

13. Найдите тангенс угла.

  Решение здесь 

14. Найдите площадь трапеции, вершины которой имеют координаты (2; 2), (8; 4), (8; 8), (2; 10). Подсказка здесь Ответ:  здесь

15.  Тип задания - круг и его элементы. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

  Подсказка здесь 

16.  Тип задания - многоугольники: вычисление длин и углов. Чему равна медиана треугольника АВС, проведенная из вершины В к стороне АС?

    Примечание. Все клетки считаем одинаковыми квадратами со стороной 1.   Решение здесь

17. На клетчатой бумаге с размером клетки 1х1 изображен четырехугольник. Найдите его площадь.

  Решение здесь

18. На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.

  Решение здесь здесь

19. На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите его площадь.

  Решение здесь здесь

В завершение еще раз напомним: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.

Чтобы продолжить подготовку к ЕГЭ 2021, перейдите по ссылкам на другие страницы сайта:

Локация Главная страница Карта сайта

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail:  [email protected]