Векторы
Локация Главная страница Карта сайта
Лайфхаки
Как считать проценты в уме
Чтобы найти 10% от числа, надо разделить данное число на 10, т. е. запятую перенести влево на один знак
Чтобы найти 5%, найдите 10% и разделите на два.
Чтобы найти 15%, найдите 10% и затем прибавьте 5%.
Чтобы найти 20%, найдите 10% и умножьте на два.
50% числа- это половина данного числа.
Чтобы найти 25%, найдите 50% и разделите на два.
Чтобы найти 60%, найдите 50% и прибавьте 10%.
Чтобы найти 75%, найдите 50%, а затем прибавьте 25% и т. д.
6 способов посчитать проценты от суммы
1. Как посчитать проценты, разделив число на 100 здесь и здесь
2. Как посчитать проценты, разделив число на 10 здесь
3. Как посчитать проценты, составив пропорцию здесь и здесь
Сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении
4. Как посчитать проценты с помощью соотношений здесь
5. Как посчитать проценты с помощью калькулятора здесь
6. Как посчитать проценты с помощью онлайн-сервисов
Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах:
Planetcalc→ Калькулятор — справочный портал→ Allcalc→
Два способа перевести обыкновенную дробь в десятичную
1. Превратите знаменатель в 10, 100 или 1 000 здесь и здесь
2. Поделите числитель на знаменатель здесь и здесь
4 способа найти периметр прямоугольника
1. Зная все или две соседние стороны здесь
2. Зная любую сторону и площадь здесь
3. Зная любую сторону и диагональ здесь
4. Зная одну любую сторону и радиус описанной окружности здесь
8 способов найти периметр треугольника
1. Как найти периметр треугольника, зная три стороны здесь
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности здесь
3. Как вычислить периметр треугольника, зная две стороны и угол между ними здесь
4. Как найти периметр равностороннего треугольника, зная одну сторону здесь
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание здесь
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту здесь
7. Как вычислить периметр прямоугольного треугольника, зная катеты здесь
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу здесь
9 способов найти радиус окружности
1. Через площадь круга здесь
2. Через длину окружности здесь
3. Через диаметр окружности здесь
4. Через диагональ вписанного прямоугольника здесь
5. Через сторону описанного квадрата здесь
6. Через стороны и площадь вписанного треугольника здесь
7. Через площадь и полупериметр описанного треугольника здесь
8. Через площадь сектора и его центральный угол здесь
9. Через сторону вписанного правильного многоугольника здесь
Веб-сервисы
Регулярно заниматься интеллектуальной зарядкой с числами можно и на математических онлайн-тренажёрах. Выбирайте необходимый вам тип действия и уровень сложности — и вперёд, к новым интеллектуальным вершинам. Вот лишь несколько вариантов.
- Математика.Club — тренажёр устного счёта.
- Школа Аристова — тренажёр устного счёта (охватывает двузначные и трёхзначные числа).
- «Развивайка» — тренировка устного счёта в пределах ста.
- 7gy.ru — тренажёр по математике (вычисления в пределах ста).
- Chisloboy — онлайн-игра на развитие скорости счёта.
- kid-mama — тренажёры по математике для 0–6 классов.
ОСИ КООРДИНАТ
Для понимания темы «вектор», надо сначала разобраться с понятием «декартовы координаты».
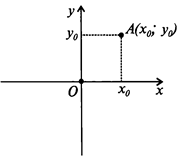
- ось x — ось абсцисс;
- ось y — ось ординат,
- точка О — начало координат.
Любой точке плоскости сопоставляются два числа:
- абсцисса x0,
- ордината y0.
Эти числа называются декартовыми координатами данной точки.
ВЕКТОР:
Вектор — направленный отрезок прямой. То есть это отрезок, для которого указано, какая из его точек является началом, а какая — концом.
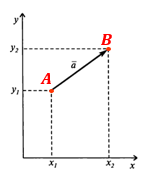
Пусть имеются две точки:
- A с координатами
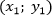
- B с координатами
.
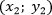- A с координатами
Тогда мы имеем вектор
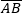, который обозначим за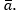
На примере вектора рассмотрим основные понятия, связанные с векторами.
Во-первых, для каждого вектора можно найти его координаты и модуль.
КООРДИНАТЫ ВЕКТОРА И МОДУЛЬ ВЕКТОРА:
Координаты вектора — разности координат конца и начала вектора. На примере вектора
его координатами будут: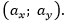
Свойства координат вектора:- Координаты вектора не изменяются при параллельном переносе.
- У равных векторов соответствующие координаты равны.
Нахождение координат вектора:
Координаты вектора
То есть, координаты вектора
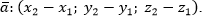
Модуль вектора — длина вектора (обозначается ). Находится как квадратный корень из суммы квадратов координат вектора.
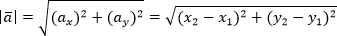
Если рассмотреть пространственный вектор, то в эти формулы добавляется третья координата — z.
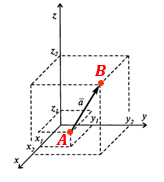
Координаты вектора
:
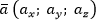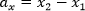
То есть, координаты вектора
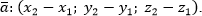
Модуль вектора
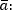
СЕРЕДИНА ВЕКТОРА:
Чтобы найти середину вектора по координатам нужно:
1. Вычислить сумму координат начала и конца вектора.
2. Разделить на два.
НА ПЛОСКОСТИ В ПРОСТРАНСТВЕ O — середина вектора 
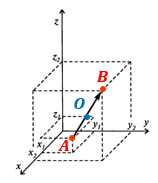
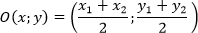
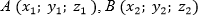
ВИДЫ ВЕКТОРОВ:
Единичный вектор — вектор, длина которого равна 1.
Нулевой вектор — отдельные точки плоскости. У такого вектора конец и начало совпадают, а его длина (его модуль) равен нулю.
Коллинеарные и компланарные векторы
Коллинеарные векторы — векторы, которые параллельны одной прямой или которые лежат на одной прямой.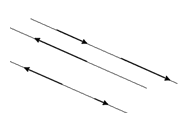 
Два коллинеарных вектора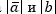
называются сонаправленными только тогда, когда их направления соответствуют друг другу:
Компланарные векторы — векторы, которые параллельны одной плоскости или которые лежат на общей плоскости. 
В любое мгновение существует плоскость одновременно параллельная двум любым векторам, поэтому два произвольных вектора являются компланарными.АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД ВЕКТОРАМИ:
ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ И ГЕОМЕТРИЧЕСКАЯ РАЗНОСТЬ ВЕКТОРОВ:
СЛОЖЕНИЕ
Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма:
=
+
.
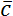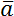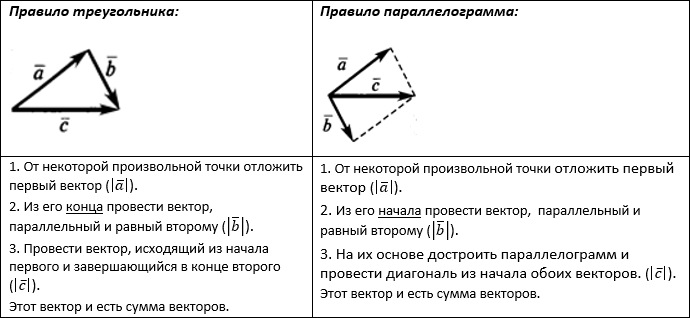
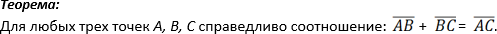
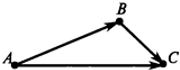
Поделитесь со своими друзьями в социальных сетях ссылкой на сайт vivat2.okis.ru
Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка тик ток