№ 8 ЕГЭ профиль / vivat2.okis.ru

Меню

№ 8 ЕГЭ профиль

Прототипы задания 8 профиля ЕГЭ - 2021(№ 13, 16 базового уровня)

Тема заданий № 8 "Стереометрия"

Типы заданий № 8: куб здесь прямоугольный параллелепипед здесь элементы составных многогранников здесь площадь поверхности составного многогранника здесь объем составного многогранника здесь призма здесь здесь здесь здесь Пирамида здесь здесь здесь комбинации тел здесь здесь цилиндр здесь конус здесь шар здесь

За задание № 8 ты можно получить 1 балл. На решение дается около 5 минут. Уровень сложности: базовый. Средний процент выполнения: в 2019 году 66.7%, в 2020 году 63,8%. Ответом к заданию 8 по математике может быть целое число или конечная десятичная дробь. Требования ФИПИ к профильному уровню здесь Соответствие заданий в КИМах базового и профильного уровня здесь

Особенности. Задания № 8 представляют собой стереометрические задачи на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть. Важно увидеть путь решения и какую формулу необходимо применить: теорема Пифагора здесь теорема косинусов здесь определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике здесь здесь формулы площадей фигур здесь формулы объѐмов тел здесь отношение площадей подобных фигур здесь отношение объѐмов подобных тел здесь

Топ-3 задач-ловушек типа № 8:1)здесь 2)здесь 3)здесь 95% учащихся ошибаются при решении прототипов таких задач. Внимательнее, пожалуйста! Можно поторопиться и получить 0 баллов за подобное задание.

Когда 0 баллов за задачу 8 гарантировано? У Вас ведь был тот самый огромный лист с формулами для задачи № 8? 100500 формул на листе, 0 формул в памяти и отсутствие желания включить мозг и подумать, как же без этого листа найти объем кубика и выяснить какую часть от этого кубика отрезали, — и минус балл у Вас в кармане.

В задании 8 рассматриваются только простейшие пространственные тела, если параллелепипед, то прямоугольный, если пирамида, то правильная. В этих случаях задача легко сводится к планиметрии.

Задачи с ответами для самостоятельного решения и самопроверки,

предлагаемые авторами ЕГЭ на экзаменах прошлых лет, а также из открытого банка ФИПИ:

1. 2021 год. Демонстрационный вариант ЕГЭ. (2016 год, основная волна). В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.

Решение здесь

ИЛИ

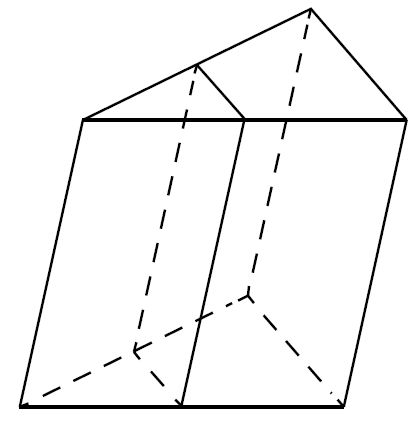
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы. Решение здесь

ИЛИ

Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1 : 2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54? Решение здесь

1. 2020 год, основная волна, Москва. Найдите объем многогранника, вершинами которого являются точки , , , прямоугольного параллелепипеда , у которого , ,

Решение здесь или здесь

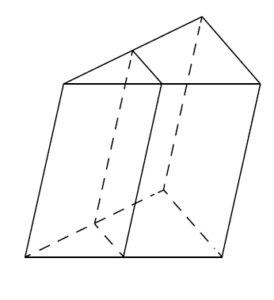
2. 2020 год, досрочная волна. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 7.

Решение здесь

3. 2019 год. Основная волна ЕГЭ. Центр. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Решение здесь

4. 2018 год. Основная волна ЕГЭ. Через среднюю линию основания треугольной призмы, объем которой равен 36, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Решение здесь

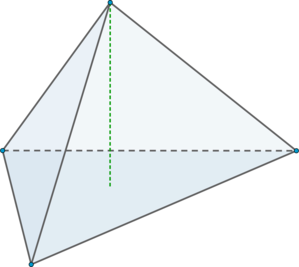
5. 2018 год. Вариант ЕГЭ. СтатГрад. Москва. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 6, а высота равна 43.

Решение здесь

6. 2018 год. Досрочная волна ЕГЭ. В сосуд цилиндрической формы налили 1000 см^3 жидкости, при этом уровень жидкости в сосуде достиг 15 см. После того, как в жидкость полностью погрузили деталь, уровень жидкости поднялся на 9 см. Чему равен объем погруженной детали? Ответ выразите в см^3.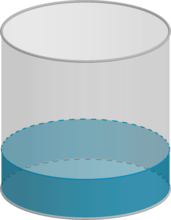
Решение здесь

7. 2018 год. Вариант ЕГЭ. СтатГрад. Москва. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).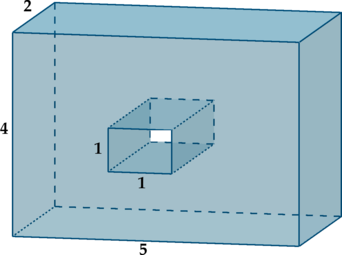
Решение здесь
8. 2017 год. Основная волна ЕГЭ. В сосуд цилиндрической формы налили воду до уровня 32 см. Какого уровня достигнет вода, если перелить её в другой сосуд цилиндрической формы, радиус основания которого в 4 раза больше радиуса основания первого сосуда.? Ответ дайте в см. Решение здесь

9. 2017 год. Основная волна ЕГЭ. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объем цилиндра, если объем конуса равен 25.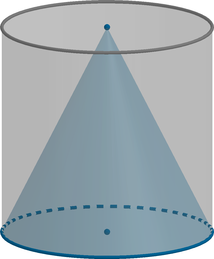

Решение здесь

10. 2017 год. Основная волна ЕГЭ. Конус и цилиндр имеют общее основание и общую высоту, равную радиусу основания (конус вписан в цилиндр). Вычислите площадь боковой поверхности цилиндра, если квадрат площади боковой поверхности конуса равна 98.
Решение здесь

11. 2017 год. Резервная волна ЕГЭ. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 7, высота призмы равна 6. Найдите ее объем.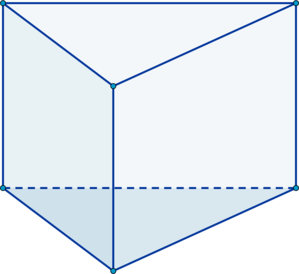
Решение здесь

12. 2017 год. Досрочная волна ЕГЭ. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Известно, что BB1=6, AB=4, A1D1=5. Найдите объем многогранника ABA1B1C1D1.

Решение здесь

13. 2017 год. Официальный пробный вариант ЕГЭ. Даны два цилиндра. Объем первого цилиндра равен 8. У второго цилиндра высота в 4 раза меньше, а радиус основания в 3 раза больше, чем у первого. Найдите объем второго цилиндра.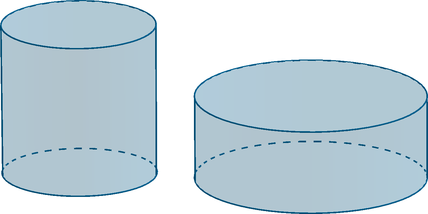
Решение здесь

14. 2016 год. Основная волна ЕГЭ. Юг. Объём треугольной пирамиды равен 94. Через вершину пирамиды и среднюю линию её основания проведена плоскость. Найдите объём отсечённой треугольной пирамиды.

Решение здесь

15. 2016 год. Досрочная волна ЕГЭ. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

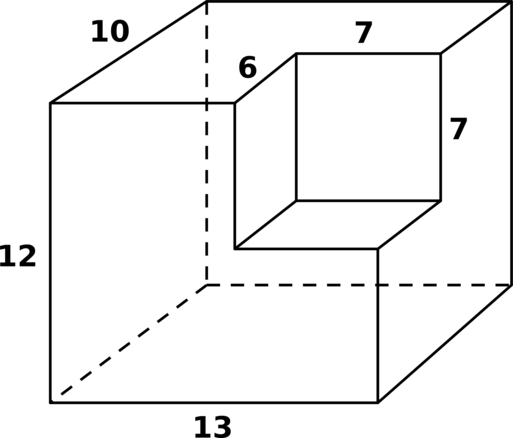
Решение здесь

16. 2015 год. Основная волна ЕГЭ. В правильной шестиугольной пирамиде боковое ребро равно 13, а сторона основания равна 5. Найдите высоту пирамиды.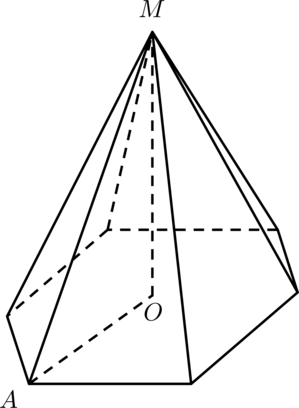
Решение здесь

17. 2015 год. Досрочная волна ЕГЭ. В правильной четырёхугольной пирамиде высота равна 3, а квадрат бокового ребра равен 27. Найдите её объём.
Решение здесь

18. 2014 год. Основная волна ЕГЭ. Запад. Даны два шара. Диаметр второго шара в 8 раз больше диаметра первого. Во сколько раз площадь поверхности второго шара больше площади поверхности первого?

Решение здесь

19. 2014 год. Основная волна ЕГЭ. Запад. Диагональ куба в квадрате равна 48 Найдите объём куба.

Решение здесь

Куб. Задача 1. Площадь поверхности куба равна 18. Найти его диагональ.

Решение здесь

Задача 2. Объем куба равен 8. Найдите площадь его поверхности. Решение здесь

Задача 3. Если каждое ребро куба увеличить на 1, то площадь его поверхности увеличится на 54. Найдите ребро куба. Решение здесь

Задача 4. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза? Решение здесь

Задача 5.

Решение здесь

Задача 6.

Решение здесь

Задача 7. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба. Решение здесь

Задача 8. Во сколько раз увеличится площадь поверхности куба, если все его ребра увеличить в 3 раза? Решение здесь

Задача 9.

Решение здесь

Задача 10. Площадь поверхности куба равна 24. Найдите его объём. Решение здесь

Куб. Задача 11. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

Решение здесь

Задача 12. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов. Решение здесь

Задача 13. Найдите площадь пространственного креста, изображенного на рисунке к задаче 12 и составленного из единичных кубов. Решение здесь

Задача с решением 14 здесь

Куб. Решение здесь

Задача 15.

Решение здесь

Задача 16.

Решение здесь

Задача 17.

Решение здесь

Задача с решением 18 здесь

Прямоугольный параллелепипед.

Задача с решением 19 здесь

Задача 20.

Решение здесь

Задача 21.

Решение здесь

Задачи с решением: Задача 22 здесь Задача 23 здесь Задача 24 здесь Задача 25 здесь Задача 26 здесь Задача 27 здесь Задача 28 здесь Задача 29 здесь Задача 30 здесь Задача 31 здесь Задача 32 здесь Задача 33 здесь здесь Задача 34 здесь Задача 35 здесь Задача 36 здесь

Площадь поверхности составного многогранника. Задача 37 здесь Задача 38 здесь Задача 39 здесь Задача 40 здесь

Комбинации тел. Задача 41.

Решение здесь
Задача с решением: 42 здесь здесь По теореме Архимеда объем цилиндра в 1,5 раза больше объёма вписанного в него шара. Ответ: 62. Задача с решением: 44 здесь

45. Стороны основания правильной четырехугольной пирамиды равны 18, боковые ребра равны 15. Найдите площадь поверхности этой пирамиды. Задача решается аналогично разобранной выше.

Чтобы продолжить подготовку к ЕГЭ 2021, перейдите по ссылкам на другие страницы сайта:

Локация Главная страница Карта сайта

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail: [email protected]

Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка тикток

KISS

Есть известный принцип, применяемый в программировании и дизайне. По-английски он звучит так: «Keep it simple,stupid!» (Не усложняй, чудило!)

Задачи 3232 - 3238 проекта "Матема"

3232. На ветке сидят 3 птицы. Все, кроме двух, вороны, все, кроме двух, воробьи, все, кроме двух,голуби. Сколько ворон, воробьёв и голубей сидят на ветке?

3233.Катя составила из цифр 1, 2, 3, 4, 5 самое большое трёхзначное и самое маленькое двузначное числа (при этом цифры в числах не повторяются), а потом записала их разность.Какое число записала Катя?

3234.27 октября 2016года у Маши родился братик Ваня. Сегодня ему исполнился 1 месяц. Какой сегоднядень недели, если 27 октября был четверг, а в октябре 31 день?

3235.Катя позвала подруг в гости. Таня решила, что пойдёт в гости к Кате, если пойдут Оля и Марина. Оля решила, что пойдёт в гости к Кате, если пойдёт Марина. Марина решила, что пойдёт в гости к Кате, если не пойдёт Оля и пойдёт Таня. Кто из девочек пойдёт в гости к Кате?

3236.Петух Петя в течение недели с 4 до 8 утра каждые полчаса по 3 раза кричал «кукареку». Сколько всего раз Петя крикнул «кукареку» за неделю?

3237.В классе 24 ученика. Половина из них девочки. Треть всех учеников пойдут сегодня вечером в кино. Известно, что 5 из них – мальчики, а остальные – девочки. Сколько девочек не пойдут сегодня в кино?

3238.По стеблю цветка ползёт гусеница. Она начала движение в понедельник в 10 часов утра. В четверг в это же время она оказалась на высоте 42 см от земли. На какой высоте окажется гусеница в воскресенье в 10 часов утра, если известно, что во вторые сутки она поднималась вдвое быстрее, чем в первые, в третьи – вдвое быстрее, чем во вторые, и так далее.

Задача 3225 - 3231 проекта "Матема"

3225.Решите уравнение $(x^{2} - x + 1)^{2} - 10 (x - 4) (x + 3) - 109 = 0$ . В ответе укажите сумму его корней.

3226.Число aa при делении на 7 дает в остатке 2 или 4. В каком из этих случаев будет больше остаток от деления числа a^2 на 7? В ответе укажите номер правильного ответа: 1 - если число aa при делении на 7 дает в остатке 2; 2 - если число aa при делении на 7 дает в остатке 4.

3227.Два пешехода должны выйти навстречу друг другу из двух пунктов, расстояние между которыми 20 км. Если первый выйдет на полчаса раньше второго, то он встретит второго пешехода через 2,5 ч после своего выхода. Если второй выйдет на 1 ч раньше первого, то он встретит первого пешехода через 2 ч 40 мин после своего выхода. Какова скорость первого пешехода (в км/ч)?

3228.Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495. Сумма цифр этого трехзначного числа равна 17, а сумма квадратов его цифр равна 109. Найти такое трехзначное число.

3229.При каких значениях параметра b корень уравнения 6−3b+4bx=4b+12x меньше 1?

3230.Диагональ равнобедренной трапеции является биссектрисой острого угла, а основания относятся как 1:2. Периметр трапеции равен 90. Найдите большую сторону трапеции.

3231.Четырехугольник PQRS вписан в окружность. Диагонали PR и QS перпендикулярны и пересекаются в точке M. Известно, что PS=13, QM=10, QR=26. Найти площадь четырехугольника PQRS.

Задачи 3218 - 3 224 проекта "Матема"

3218.Через 52 месяца Майе исполнится ровно 7 лет. Сколько лет и сколько месяцев сейчас Майе?

3219.Пилот Саша получил задание перевезти 19 пассажиров с аэродрома Дракино на аэродром Конаково. Он запустил вертолёт на аэродроме Дракино и готов начать перевозку. Сколько посадок придётся сделать вертолёту, чтобы справиться с задачей, если всего он вмещает 5 человек, включая пилота?

3220. Маша собиралась с родителями на море. Она достала свой чемодан и поняла, что забыла код. Она помнит, что код состоит из цифр 2, 5 и 6 и что они не повторяются, но не может вспомнить их порядок.Каково максимальное количество времени, которое понадобится Маше, чтобы подобрать код,если на проверку одного кода у неё уходит 10 секунд?

3221.Аня шила платки.Сначала она разрезала ткань на 27 одинаковых квадратов, затем решила одну треть квадратов разрезать ещё на 4 части, чтобы получились носовые платочки. Из другой трети квадратов Аня сшила платки побольше, а последнюю треть квадратов она решила разрезать на 2 части и сделать шарфики. Сколько платков (носовых платков и платков побольше) и сколько шарфиков сшила Аня?

3222.У царя Додона есть роскошный сад прямоугольной формы. Злой колдун за одну ночь уменьшил сад царя Додона в 9 раз. Царь в отчаянии! А можешь ли ты сказать царю, как изменились длины сторон его сада?

3223.Встретились два кота. Кот Вася говорит: «Я за 5 недель наловлю 10 килограммов рыбы». А кот Филя отвечает: «А я наловлю столько же рыбы за 2 недели».За сколько дней они вместе наловят 10 килограммов рыбы?

3224.На школьном празднике Маша, Катя и Таня раздавали ученикам билеты в театр. Маша раздала половину всех билетов и ещё 2, Катя – половину оставшихся билетов, а Таня раздала ребятам последние 9 билетов. Сколько всего билетов раздавали ученикам на празднике?

Задача 3211 - 3217 проекта "Матема"

3211. Разность кубов двух последовательных натуральных чисел равна $331$ . Чему равен куб суммы этих чисел?

3212.При каком значении параметра a уравнение |x2−2x−3|=a имеет три корня?

3213.В трёхзначном числе зачеркнули среднюю цифру. Полученное двузначное число оказалось в 6 раз меньше исходного трёхзначного. Найдите это трёхзначное число.

3214.Стоимость билета в кино была 1200 рублей. После снижения стоимости количество посетителей увеличилось 1,5 раза и сбор увеличился на 25%. На сколько рублей была снижена стоимость билета? Дайте ответ в рублях.

3215.На часах со стрелками ровно 10. Через сколько минут стрелки часов часовая и минутная совпадут в первый раз? Дайте ответ в минутах, округлите до целых.

3216.В коробке 6 красных, 7 зелёных, 8 синих и 9 жёлтых карандашей. В темноте из коробки берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них обязательно было 3 красных и 2 зелёных карандаша?

3217.Из посёлка в город идёт автобус, и каждые 6 минут он встречает автобус, который идёт из города в посёлок, и скорость которого в 1,5 раза больше. Сколько автобусов в час приходит из города в посёлок?