№ 6 ЕГЭ профиль / vivat2.okis.ru

Меню

№ 6 ЕГЭ профиль

Прототипы задания 6 профиля ЕГЭ - 2021 (№ 8, 15 базового уровня)

Тема заданий № 6 "Планиметрия". Типы заданий № 6: Решение прямоугольного треугольника здесь и здесь и здесь и здесь здесь здесь здесь здесь Решение равнобедренного треугольника здесь и здесь Треугольники общего вида здесь и здесь и здесь здесь здесь здесь Параллелограммы здесь Трапеция здесь и здесь Центральные и вписанные углы здесь и здесь Касательная, хорда, секущая здесь Вписанные окружности здесь и здесь Описанные окружности здесь и здесь

За задание № 6 можно получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый. Средний процент выполнения: в 2019 году 80.6%, в 2020 году 76,8%. Ответ к заданию - целое число или конечная десятичная дробь. Требования ФИПИ к профильному уровню здесь Соответствие заданий в КИМах базового и профильного уровня здесь

Типичные ошибки при решении задания №6 в ЕГЭ: выпускник чаще всего может перепутать катет с гипотенузой, не знает или неверно записывает отношение сторон при использовании тригонометрических функций. И помните при правильном решении ответ получается точно без корня.

Большая часть заданий этого типа являются несложными, однако объем теоретического материала, которым надо владеть, достаточно обширен. Определения, теоремы и формулы следует выучить и постоянно повторять, проверяя себя. В заданиях № 6 содержатся основы геометрии. Чаще всего здесь встречаются задания на решение треугольников, но знать надо все фигуры планиметрии: виды треугольников здесь здесь понятия биссектрисы, медианы, высоты здесь тригонометрические функции и их значения здесь здесь основное тригонометрическое тождество здесь формулы приведения здесь теорема Пифагора и теорема косинусов здесь четырехугольники здесь здесь здесь правильный шестиугольник здесь площади многоугольников здесь здесь окружность здесь здесь здесь здесь здесь здесь здесь здесь векторы здесь здесь здесь здесь здесь

Рекомендация. Рисунок в геометрической задаче нужно воспринимать как изображение взаимного расположения элементов, но нельзя относиться к нему как к чертежу, где соблюдены все размеры. При подготовке к экзамену можно нарисовать свой рисунок, и уже с использованием этого рисунка решать задачу. Работа с новым рисунком позволит исключить ошибку, связанную с невнимательностью или приписыванием данной фигуре несуществующего свойства (например, что треугольник ABC– равносторонний). Чтобы решить задание 6 необходимо знать: 1)способы нахождения длин и углов многоугольника 2) формулы вычисления площадей многоугольника 3) золотой и серебряный треугольники здесь 4) нахождение тригонометрических функций здесь здесь здесь 5) таблица основных значений тригонометрических функций здесь 6) основное тригонометрическое тождество здесь

Тригонометрические функции острого угла прямоугольного треугольника–это не только часть планиметрических задач №3 и №6, но и ряд задач про геометрический смысл производной (№7), задачи, где требуется вычислить значения тригонометрических функций (№ 9 и даже № 10). Один из самых проблемных видов шестого задания про высоту, проведённую в прямоугольном треугольнике к гипотенузе. В задачах этого типа нужен навык "входить в треугольник", нужен навык определения в какой именно треугольник входить, и когда, и для чего. Проблемные задачи № 6 с высотой в прямоугольном треугольнике: 1)здесь 2)здесь 3)здесь 4)здесь 5)здесь 6)здесь При решении № 6 от абстрактного вопроса по типу «найдите площадь» перейдите к более четкому пониманию того, чего вам не хватает для ответа на поставленный вопрос. Например, если в треугольнике известно основание, но не известна высота, значит, для нахождения площади нужно найти высоту. Определив, чего именно вам не хватает, вы уже на полпути к успеху. После того как на чертеже отражены все данные, и вы знаете, что вам нужно найти, необходимо определить связующее звено между тем, что дано, и тем, что необходимо найти. Таким связующим звеном может быть некоторый переходный элемент, например, угол, значение которого вы можете найти. Если вам не удалось найти связующее звено, вспомните всю теорию, которая относится к тому, что вам дано или к тому, что нужно найти.

Тесты: 1)здесь подсказка ответ 2)здесь ответ 3)здесь ответ 4) здесь решение

Диагностическая работа,

содержащая тригонометрические задачи, разбитые на шесть различных типов по три задачи в каждом.Для тех, кто хочет проверить правильность решения предложенных задач или убедиться в верности полученного ответа,приводятся их решения и даются ответы.

1. Нахождение значений тригонометрических функций острых углов прямоугольного треугольника

1.1. В треугольнике ABC угол C равен 90о, AB = 10, AC = 8. Найдите sin A. Решение здесь

1.2. В треугольнике ABC угол C равен 90о, sin A = 0,6.Найдите cos A. Решение здесь

1.3. В треугольнике ABC угол C равен 90о, высота CH равна 6, AC = 10. Найдите tg A. Решение здесь

2. Нахождение значений тригонометрических функций острых углов равнобедренного треугольника

2.1. В треугольнике ABC AC = BC = 10, AB = 12. Найдите sin A. Решение здесь

2.2. В треугольнике ABC AC = BC, AB = 10, высота AH равна 8.Найдите cos A. Решение здесь здесь

2.3. В треугольнике ABC AB = BC, высота CH равна 8, квадрат AC = 320. Найдите тангенс угла ACB. Решение здесь

3. Нахождение значений тригонометрических функций тупых углов

3.1. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите синус внешнего угла при вершине A. Решение здесь

3.2. В треугольнике ABC угол C равен 90о, sin A = 0,6. Найдите косинус внешнего угла при вершине A. Решение здесь

3.3. В треугольнике ABC угол C равен 90о, AB = 10, AC = 8. Найдите тангенс внешнего угла при вершине A. Решение здесь

4. Нахождение тригонометрических функций углов, изображенных на клетчатой бумаге

4.1. Найдите синус угла AOB. В ответе укажите значение синуса,умноженное на квадратный корень из 8. Рисунок здесь Решение здесь

4.2. Найдите тангенс угла AOB. Рисунок здесь Решение здесь

4.3. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на квадратный корень из 8. Рисунок здесь Решение здесь

5. Нахождение элементов прямоугольных треугольников

5.1. В треугольнике ABC угол C равен 90о, BC = 4, sin A = 0,8.Найдите AB. Решение здесь

5.2. В треугольнике ABC угол C равен 90о, tg A = 0,75, AC = 8.Найдите AB. Решение здесь здесь

5.3. В треугольнике ABC угол C равен 90о, CH –высота, BC = 6, cos A = 0,8. Найдите CH. Решение здесь

6. Нахождение элементов равнобедренных треугольников

6.1. В треугольнике ABC AC = BC = 10, sin A = 0,8. Найдите AB. Решение здесь здесь

6.2. В треугольнике ABC AC = BC, AB = 10, cos A = 0,6. Найдите высоту AH. Решение здесь здесь

6.3. В треугольнике ABC AB = BC, высота CH равна 5, квадрат tg C =1/3 .Найдите AC. Решение здесь здесь

Задачу 6 легко можно завалить, если перепутать противолежащий катет с прилежащим, описанную окружность с вписанной, острый угол с тупым, если не помните ни одну из формул площади, и даже не пытаетесь вывести их самостоятельно.

Задачи с ответами для самостоятельного решения и самопроверки,

предлагаемые авторами ЕГЭ на экзаменах прошлых лет, а также из открытого банка ФИПИ:

1. 2021 год. Демонстрационный вариант ЕГЭ. Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32°. Ответ дайте в градусах. Решение здесь

ИЛИ

Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE. Решение здесь

ИЛИ

В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах. Решение здесь

ИЛИ

Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма. Решение здесь

1. 2020 год. Основная волна. Москва. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение здесь или здесь

2. 2020 год. Досрочная волна.

В треугольнике ABC сторона AB равна 2√3, угол C равен 120 градусов. Найдите радиус описанной около этого треугольника окружности.

Решение здесь

3. 2019 год. Основная волна ЕГЭ. Центр.

Угол между стороной и диагональю ромба равен Найдите острый угол ромба.

Решение здесь

4. 2018 год. Основная волна ЕГЭ.

Отрезки AC и BD – диаметры окружности с центром O. Угол AOD равен 46∘. Найдите вписанный угол DBC. Ответ дайте в градусах.

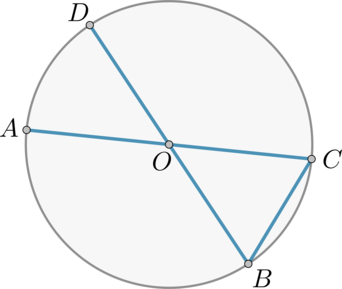Решение здесь

5. 2017 год. Основная волна ЕГЭ. Дан параллелограмм со сторонами 21 и 28. К меньшей стороне проведена высота, длина которой равна 20. Найдите длину высоты, проведенной к большей стороне.
Решение здесь

6. 2016 год. Основная волна ЕГЭ. Юг. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение здесь

1. Длина боковой стороны равнобедренного треугольника равна 5 см, а его основание на 1 см длиннее. Чему равна площадь треугольника?

Решение здесь

2. В четырехугольник АВСD вписана окружность, АВ =8, ВС = 10 и СD = 37. Найдите четвертую сторону четырехугольника.

Решение здесь

3. В треугольнике ABC AC = BC = 2√2, угол C равен 135°. Найдите высоту AH.

Подсказка здесь Ответ: здесь

4. Диагонали ромба относятся как 1 : 9. Периметр ромба равен 164. Найдите высоту ромба.

Подсказка 1 здесь Подсказка 2 здесь Ответ: здесь

5. В равнобедренном треугольнике ABC c основанием AC боковая сторона АВ равна 15,а высота, проведенная к основанию, равна 9. Найдите косинус угла А.

Ответ: здесь

6.

Ответ: здесь

7.

Ответ: здесь

8.

Ответ: здесь

9. В треугольнике АВС угол С равен 90 градусов, АВ =15 , ВС= 9. Найти cosA

Ответ: здесь

10.

Ответ: здесь

11.

Ответ: здесь

12.

Ответ: здесь

Для решения следующей задачи необходимо знать, что: 1) Сумма противолежащих углов четырехугольника, вписанного в окружность, равна 180. 2) Сумма углов треугольника равна 180. 3) Вписанные углы, опирающиеся на одну и ту же хорду, равны.

13.

Ответ: здесь

14. Угол при вершине, противоположной основанию равнобедренного треугольника, равен 30 градусов. Боковая сторона треугольника равна 18. Найдите площадь этого треугольника.

Ответ здесь

15. Угол при вершине, противоположной основанию равнобедренного треугольника, равен 30. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника. Ответ здесь

16. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2 : 7, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 44. Решение здесь

Чтобы продолжить подготовку к ЕГЭ 2021, перейдите по ссылкам на другие страницы сайта:

Локация Главная страница Карта сайта

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней. E-mail: [email protected]

Во всем мне хочется дойти

До самой сути.

Б. Л. Пастернак, «Во всем мне хочется дойти...»

Вопрос 1 задала Елизавета Олехнович (5 класс гимназии №1 г. Ивье).

Меня очень заинтересовала одна задача. Вот ее условие.

Частное двух чисел равно 36. Делимое уменьшили в 4 раза, а делитель уменьшили в 9 раз. Каким будет новое частное?

Подскажите, как к ней подступиться?

Консультация. Когда говорим о делимом, делителе и частном, то должны вспомнить, что делимое:делитель =частное или a:b=p.

Заметим, во сколько раз уменьшаем делимое, во столько же раз уменьшается и частное, ведь число а приходится сначала разделить на 4, а затем разделить на то же самое число b и в результате получится число в 4 раза меньшее 36, т. е. 36:4 = 9.

Если делитель уменьшить в несколько раз, то частное увеличится во столько же раз, ведь сначала надо число b разделить на 9, а потом то же самое число а разделить на меньшее в 9 раз число, т. е. 36·9 = 324.

Если же делимое уменьшить в 4 раза, а делитель уменьшить в 9 раз, то последовательно получаем: 36:4·9 = 81.

Ответ: 81.

Аналогично, во сколько раз увеличивается делимое, во столько же раз увеличивается частное, а при увеличении в несколько раз делителя частное уменьшается во столько же раз.

Если делимое увеличивается (уменьшается) в несколько раз, то частное увеличивается (уменьшается) во столько же раз.

Если делитель увеличивается (уменьшается) в несколько раз, то частное уменьшается (увеличивается) во столько же раз.

Используя эти факты, можно решить многие задачи такого же типа.

3.142.Как изменится частное, если делимое увеличить:

1) в 6 раз, а делитель увеличить в 3 раза;

2) в 8 раз, а делитель увеличить в 2 раза?

3.143. Как можно уменьшить делимое и делитель, чтобы частное:

1) увеличить в 5 раз;

2) уменьшить в 4 раза?

Частное двух чисел равно 27. Делимое уменьшили в 3 раза, а делитель уменьшили в 5 раз. Каким будет новое частное?

Частное двух чисел равно 45. Делимое увеличили в 4 раза, а делитель уменьшили в 9 раз. Каким будет новое частное?

Частное двух чисел равно 18. Делимое увеличили в 4 раза, а делитель увеличили в 9 раз. Каким будет новое частное?

Частное можно найти и по-другому. Поскольку указанное свойство верно для любых чисел, то достаточно построить соответствующий пример. В последней задаче данное частное может быть представлено в виде 18:1 = 18. По условию (18·4): (1·9) = 72:9 = 8. Ответ: 8.

Создано на конструкторе сайтов Okis при поддержке Flexsmm - накрутка instagram

KISS

Есть известный принцип, применяемый в программировании и дизайне. По-английски он звучит так: «Keep it simple,stupid!» (Не усложняй, чудило!)

Задачи 3232 - 3238 проекта "Матема"

3232. На ветке сидят 3 птицы. Все, кроме двух, вороны, все, кроме двух, воробьи, все, кроме двух,голуби. Сколько ворон, воробьёв и голубей сидят на ветке?

3233.Катя составила из цифр 1, 2, 3, 4, 5 самое большое трёхзначное и самое маленькое двузначное числа (при этом цифры в числах не повторяются), а потом записала их разность.Какое число записала Катя?

3234.27 октября 2016года у Маши родился братик Ваня. Сегодня ему исполнился 1 месяц. Какой сегоднядень недели, если 27 октября был четверг, а в октябре 31 день?

3235.Катя позвала подруг в гости. Таня решила, что пойдёт в гости к Кате, если пойдут Оля и Марина. Оля решила, что пойдёт в гости к Кате, если пойдёт Марина. Марина решила, что пойдёт в гости к Кате, если не пойдёт Оля и пойдёт Таня. Кто из девочек пойдёт в гости к Кате?

3236.Петух Петя в течение недели с 4 до 8 утра каждые полчаса по 3 раза кричал «кукареку». Сколько всего раз Петя крикнул «кукареку» за неделю?

3237.В классе 24 ученика. Половина из них девочки. Треть всех учеников пойдут сегодня вечером в кино. Известно, что 5 из них – мальчики, а остальные – девочки. Сколько девочек не пойдут сегодня в кино?

3238.По стеблю цветка ползёт гусеница. Она начала движение в понедельник в 10 часов утра. В четверг в это же время она оказалась на высоте 42 см от земли. На какой высоте окажется гусеница в воскресенье в 10 часов утра, если известно, что во вторые сутки она поднималась вдвое быстрее, чем в первые, в третьи – вдвое быстрее, чем во вторые, и так далее.

Задача 3225 - 3231 проекта "Матема"

3225.Решите уравнение $(x^{2} - x + 1)^{2} - 10 (x - 4) (x + 3) - 109 = 0$ . В ответе укажите сумму его корней.

3226.Число aa при делении на 7 дает в остатке 2 или 4. В каком из этих случаев будет больше остаток от деления числа a^2 на 7? В ответе укажите номер правильного ответа: 1 - если число aa при делении на 7 дает в остатке 2; 2 - если число aa при делении на 7 дает в остатке 4.

3227.Два пешехода должны выйти навстречу друг другу из двух пунктов, расстояние между которыми 20 км. Если первый выйдет на полчаса раньше второго, то он встретит второго пешехода через 2,5 ч после своего выхода. Если второй выйдет на 1 ч раньше первого, то он встретит первого пешехода через 2 ч 40 мин после своего выхода. Какова скорость первого пешехода (в км/ч)?

3228.Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495. Сумма цифр этого трехзначного числа равна 17, а сумма квадратов его цифр равна 109. Найти такое трехзначное число.

3229.При каких значениях параметра b корень уравнения 6−3b+4bx=4b+12x меньше 1?

3230.Диагональ равнобедренной трапеции является биссектрисой острого угла, а основания относятся как 1:2. Периметр трапеции равен 90. Найдите большую сторону трапеции.

3231.Четырехугольник PQRS вписан в окружность. Диагонали PR и QS перпендикулярны и пересекаются в точке M. Известно, что PS=13, QM=10, QR=26. Найти площадь четырехугольника PQRS.

Задачи 3218 - 3 224 проекта "Матема"

3218.Через 52 месяца Майе исполнится ровно 7 лет. Сколько лет и сколько месяцев сейчас Майе?

3219.Пилот Саша получил задание перевезти 19 пассажиров с аэродрома Дракино на аэродром Конаково. Он запустил вертолёт на аэродроме Дракино и готов начать перевозку. Сколько посадок придётся сделать вертолёту, чтобы справиться с задачей, если всего он вмещает 5 человек, включая пилота?

3220. Маша собиралась с родителями на море. Она достала свой чемодан и поняла, что забыла код. Она помнит, что код состоит из цифр 2, 5 и 6 и что они не повторяются, но не может вспомнить их порядок.Каково максимальное количество времени, которое понадобится Маше, чтобы подобрать код,если на проверку одного кода у неё уходит 10 секунд?

3221.Аня шила платки.Сначала она разрезала ткань на 27 одинаковых квадратов, затем решила одну треть квадратов разрезать ещё на 4 части, чтобы получились носовые платочки. Из другой трети квадратов Аня сшила платки побольше, а последнюю треть квадратов она решила разрезать на 2 части и сделать шарфики. Сколько платков (носовых платков и платков побольше) и сколько шарфиков сшила Аня?

3222.У царя Додона есть роскошный сад прямоугольной формы. Злой колдун за одну ночь уменьшил сад царя Додона в 9 раз. Царь в отчаянии! А можешь ли ты сказать царю, как изменились длины сторон его сада?

3223.Встретились два кота. Кот Вася говорит: «Я за 5 недель наловлю 10 килограммов рыбы». А кот Филя отвечает: «А я наловлю столько же рыбы за 2 недели».За сколько дней они вместе наловят 10 килограммов рыбы?

3224.На школьном празднике Маша, Катя и Таня раздавали ученикам билеты в театр. Маша раздала половину всех билетов и ещё 2, Катя – половину оставшихся билетов, а Таня раздала ребятам последние 9 билетов. Сколько всего билетов раздавали ученикам на празднике?

Задача 3211 - 3217 проекта "Матема"

3211. Разность кубов двух последовательных натуральных чисел равна $331$ . Чему равен куб суммы этих чисел?

3212.При каком значении параметра a уравнение |x2−2x−3|=a имеет три корня?

3213.В трёхзначном числе зачеркнули среднюю цифру. Полученное двузначное число оказалось в 6 раз меньше исходного трёхзначного. Найдите это трёхзначное число.

3214.Стоимость билета в кино была 1200 рублей. После снижения стоимости количество посетителей увеличилось 1,5 раза и сбор увеличился на 25%. На сколько рублей была снижена стоимость билета? Дайте ответ в рублях.

3215.На часах со стрелками ровно 10. Через сколько минут стрелки часов часовая и минутная совпадут в первый раз? Дайте ответ в минутах, округлите до целых.

3216.В коробке 6 красных, 7 зелёных, 8 синих и 9 жёлтых карандашей. В темноте из коробки берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них обязательно было 3 красных и 2 зелёных карандаша?

3217.Из посёлка в город идёт автобус, и каждые 6 минут он встречает автобус, который идёт из города в посёлок, и скорость которого в 1,5 раза больше. Сколько автобусов в час приходит из города в посёлок?